Zernike Polynomials Wikiwand

Zernike Polynomials Wikiwand In mathematics, the zernike polynomials are a sequence of polynomials that are orthogonal on the unit disk. named after optical physicist frits zernike, laureate of the 1953 nobel prize in physics and the inventor of phase contrast microscopy, they play important roles in various optics branches such as beam optics and imaging. the first 21. Zernike polynomials have the property of being limited to a range of −1 to 1, i.e. . the radial polynomials are defined as. for an even number of n − m, while it is 0 for an odd number of n − m. a special value is.

File Zernike Polynomials2 Png Wikipedia Download wolfram notebook. the zernike polynomials are a set of orthogonal polynomials that arise in the expansion of a wavefront function for optical systems with circular pupils. the odd and even zernike polynomials are given by. (1) where the radial function is defined for and integers with by. (2). The coefficients of the orthogonal expansion of an aberration function in terms of the zernike polynomials are related to the so called primary aberrations (such as astigmatism, coma, distortion), see , chap. 5. Zernike polynomials 1 introduction often, to aid in the interpretation of optical test results it is convenient to express wavefront data in polynomial form. zernike polynomials are often used for this purpose since they are made up of terms that are of the same form as the types of aberrations often observed in optical tests (zernike, 1934). Zernike equations. analytical equations for the first 37 zernike polynomials are provided below using polar coordinates ρ and θ with 0 ≤ ρ ≤ 1. following the convention of noll [3], each term is normalized so the root mean square (rms) of the data within the circular region is equal to 1. z1 = 1. z2 = 2 ρ cos (θ).
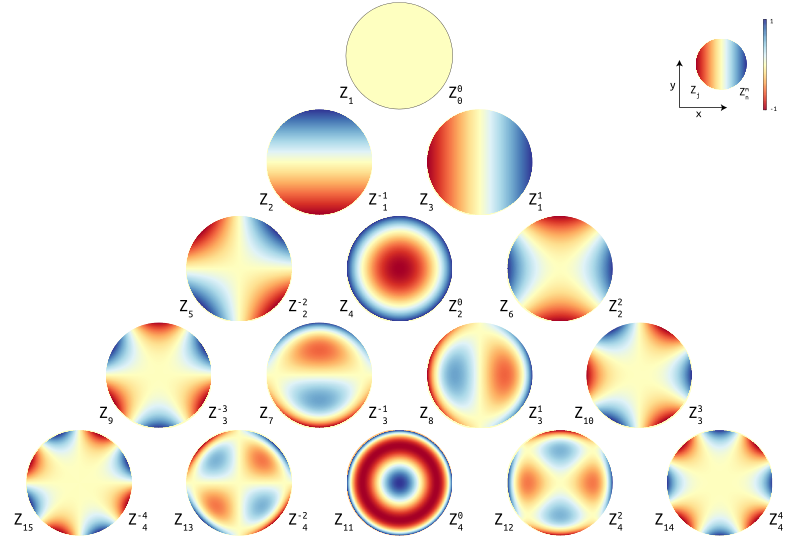
Zernike Polynomials Zernike polynomials 1 introduction often, to aid in the interpretation of optical test results it is convenient to express wavefront data in polynomial form. zernike polynomials are often used for this purpose since they are made up of terms that are of the same form as the types of aberrations often observed in optical tests (zernike, 1934). Zernike equations. analytical equations for the first 37 zernike polynomials are provided below using polar coordinates ρ and θ with 0 ≤ ρ ≤ 1. following the convention of noll [3], each term is normalized so the root mean square (rms) of the data within the circular region is equal to 1. z1 = 1. z2 = 2 ρ cos (θ). Zernike polynomials: evaluation, quadrature, and interpolationzernike polynomials are a basis of orthogonal polynomials on the unit d. sk that are a natural basis for representing smooth functions. they arise in a nu. ber of applications including optics and atmospheric sciences. in this paper, we provide a self contained reference on zernike. Zernike polynomials over circular pupils are called zernike circle polynomials or simply zernike polynomials. they are defined over a unit disk and can be most conveniently expressed in polar coordinates ( ρ, θ ), where ρ is the normalized radial coordinate (0 ⩽ ρ ⩽ 1) and θ is the polar angle measured counterclockwise from the x.

Comments are closed.