Zernike Polynomials

File Zernike Polynomials2 Png Wikipedia Zernike polynomials are orthogonal polynomials on the unit disk, named after optical physicist frits zernike. they have various applications in optics, such as beam optics and imaging, and can be represented by different indices and formulas. Learn about the properties, orthogonality, and calculation of zernike polynomials, a set of orthogonal polynomials used to represent wavefront data. see examples of zernike polynomials in polar and cartesian coordinates for different degrees and orders.

Zernike Polynomials Wikiwand Learn about the zernike polynomials, a set of orthogonal polynomials used to expand wavefront functions for optical systems with circular pupils. find definitions, properties, recurrence relations, aberrations, and examples of zernike polynomials. Zernike polynomials are a common tool for describing optical wavefronts and aberrations. learn about their numbering scheme, orthogonal basis, calculation accuracy and equations for the first 37 terms. Zernike polynomials are orthogonal polynomials on the disc, used to approximate functions such as optical aberrations. they are defined by complex coordinates and a weight function, and have various properties and applications. Learn about the mathematical functions developed by frits zernike to describe the diffracted wavefront in phase contrast imaging. find out how they are used in optical design, testing, surface fitting and wavefront analysis, and compare different sets and standards of zernike polynomials.
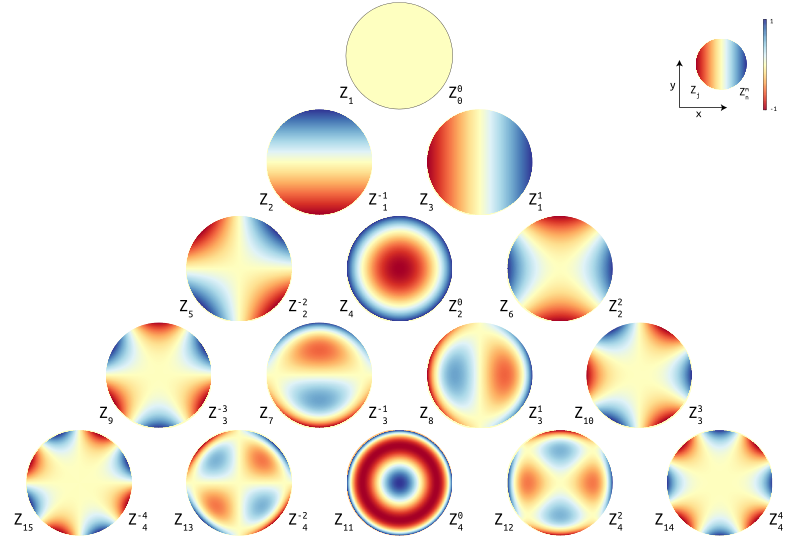
Zernike Polynomials Zernike polynomials are orthogonal polynomials on the disc, used to approximate functions such as optical aberrations. they are defined by complex coordinates and a weight function, and have various properties and applications. Learn about the mathematical functions developed by frits zernike to describe the diffracted wavefront in phase contrast imaging. find out how they are used in optical design, testing, surface fitting and wavefront analysis, and compare different sets and standards of zernike polynomials. A technical report on zernike polynomials, a basis of orthogonal polynomials on the unit disk. it covers their mathematical properties, numerical algorithms, and applications in optics and atmospheric sciences. Zernike polynomials over circular pupils are called zernike circle polynomials or simply zernike polynomials. they are defined over a unit disk and can be most conveniently expressed in polar coordinates ( ρ, θ ), where ρ is the normalized radial coordinate (0 ⩽ ρ ⩽ 1) and θ is the polar angle measured counterclockwise from the x.
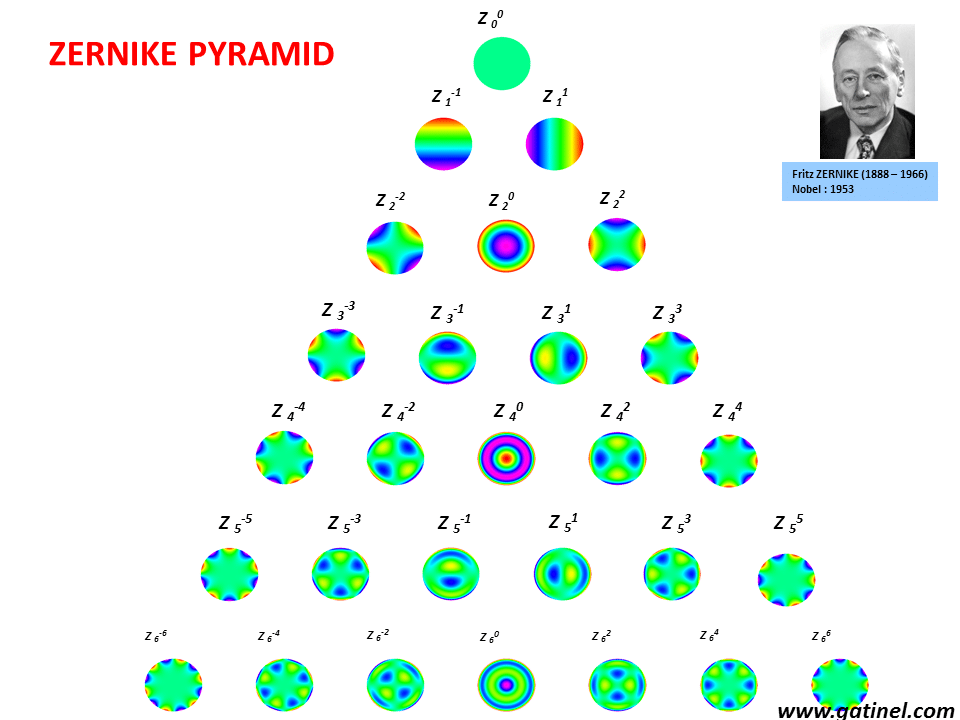
Zernike Polynomials Docteur Damien Gatinel A technical report on zernike polynomials, a basis of orthogonal polynomials on the unit disk. it covers their mathematical properties, numerical algorithms, and applications in optics and atmospheric sciences. Zernike polynomials over circular pupils are called zernike circle polynomials or simply zernike polynomials. they are defined over a unit disk and can be most conveniently expressed in polar coordinates ( ρ, θ ), where ρ is the normalized radial coordinate (0 ⩽ ρ ⩽ 1) and θ is the polar angle measured counterclockwise from the x.

Comments are closed.