Work Out Angles How To Work Out

How To Work Out Angles In A Triangle With Algebra Gcse Maths Grade 5 An exterior angle of a triangle is equal to the sum of the opposite interior angles. every triangle has six exterior angles (two at each vertex are equal in measure). the exterior angles, taken one at each vertex, always sum up to 360 ° 360\degree 360°. an exterior angle is supplementary to its adjacent triangle interior angle. Top answerer. the sum of the six interior angles of a regular polygon is (n 2) (180°), where n is the number of sides. therefore, in a hexagon the sum of the angles is (4) (180°) = 720°. all the angles are equal, so divide 720° by 6 to get 120°, the size of each interior angle. not helpful 29 helpful 27.
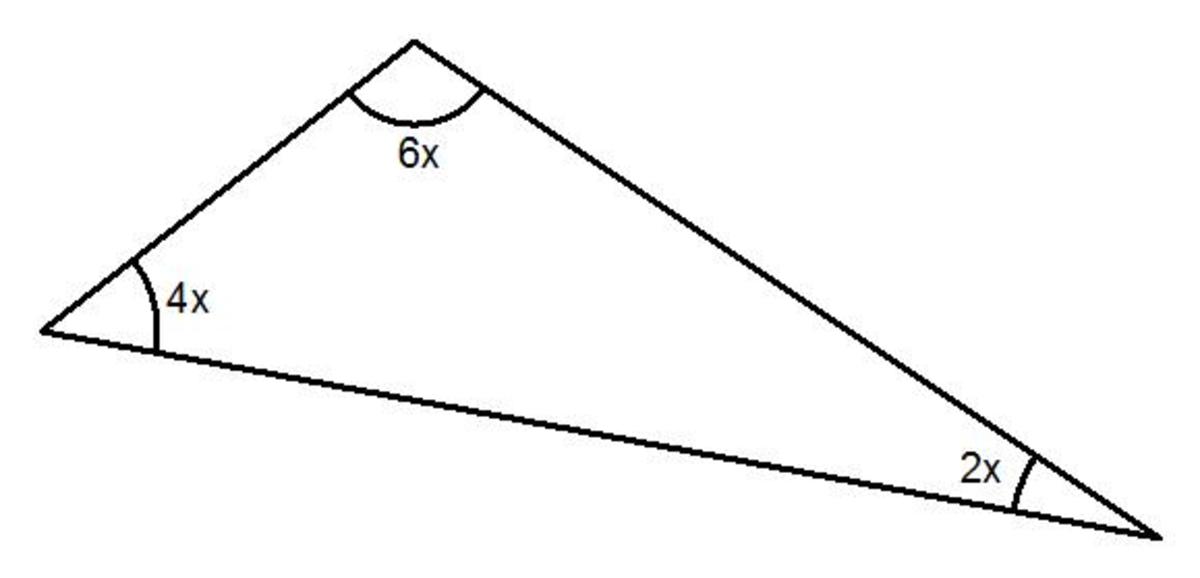
How To Work Out The Angles In An Algebraic Triangle Owlcation Find the angle of elevation of the plane from point a on the ground. step 1 the two sides we know are o pposite (300) and a djacent (400). step 2 sohcah toa tells us we must use t angent. step 3 calculate opposite adjacent = 300 400 = 0.75. step 4 find the angle from your calculator using tan 1. If the straight line or half turn is divided into two angles, and we know one of the angles, we can work out the other. here 120° 60° = 180°. if we just had information on one of the angles e. Angle rules. we can use angle rules to work out missing angles. angle rules are facts that we can apply to calculate missing angles in a diagram. the five key angle facts that are used widely within the topic are: angles on a straight line; the sum of angles on a straight line is always equal to \bf{180^{o}.}. Find the size of each angle in this right angled triangle. add the expressions for each angle. put the simplified expression equal to 180º 180º. solve the equation. work out the angles. \begin {array} {l} 3 \times 14 25=67\\\\ 2 \times 14 5=23 \end {array} the three angles are 23º 23º, 67º 67º and 90º 90º.

How To Work Out The Angle Between 2 Regular Polygons Shapes Youtube Angle rules. we can use angle rules to work out missing angles. angle rules are facts that we can apply to calculate missing angles in a diagram. the five key angle facts that are used widely within the topic are: angles on a straight line; the sum of angles on a straight line is always equal to \bf{180^{o}.}. Find the size of each angle in this right angled triangle. add the expressions for each angle. put the simplified expression equal to 180º 180º. solve the equation. work out the angles. \begin {array} {l} 3 \times 14 25=67\\\\ 2 \times 14 5=23 \end {array} the three angles are 23º 23º, 67º 67º and 90º 90º. 1. angles add to 180°: a b c = 180°. when you know two angles you can find the third. 2. law of sines (the sine rule): a sin (a) = b sin (b) = c sin (c) when there is an angle opposite a side, this equation comes to the rescue. note: angle a is opposite side a, b is opposite b, and c is opposite c. Use your knowledge about isosceles triangles two angles are always the same size. find out what the total missing value is first: 180° 50° = 130°. angles d and e must now both equal 130.

Angles Textbook Exercise Corbettmaths 1. angles add to 180°: a b c = 180°. when you know two angles you can find the third. 2. law of sines (the sine rule): a sin (a) = b sin (b) = c sin (c) when there is an angle opposite a side, this equation comes to the rescue. note: angle a is opposite side a, b is opposite b, and c is opposite c. Use your knowledge about isosceles triangles two angles are always the same size. find out what the total missing value is first: 180° 50° = 130°. angles d and e must now both equal 130.

Comments are closed.