Why Do We Use The Fourier Transform

Electrical Engineering Ch 19 Fourier Transform 1 Of 45 What Is A The fourier transform: the fourier transform can be viewed as an extension of the above fourier series to non periodic functions. for completeness and for clarity, i'll define the fourier transform here. if x(t) is a continuous, integrable signal, then its fourier transform, x(f) is given by. x(f) = ∫rx(t)e − ȷ2πft dt, ∀f ∈ r. A complicated signal can be broken down into simple waves. this break down, and how much of each wave is needed, is the fourier transform. fourier transforms (ft) take a signal and express it in terms of the frequencies of the waves that make up that signal. sound is probably the easiest thing to think about when talking about fourier transforms.
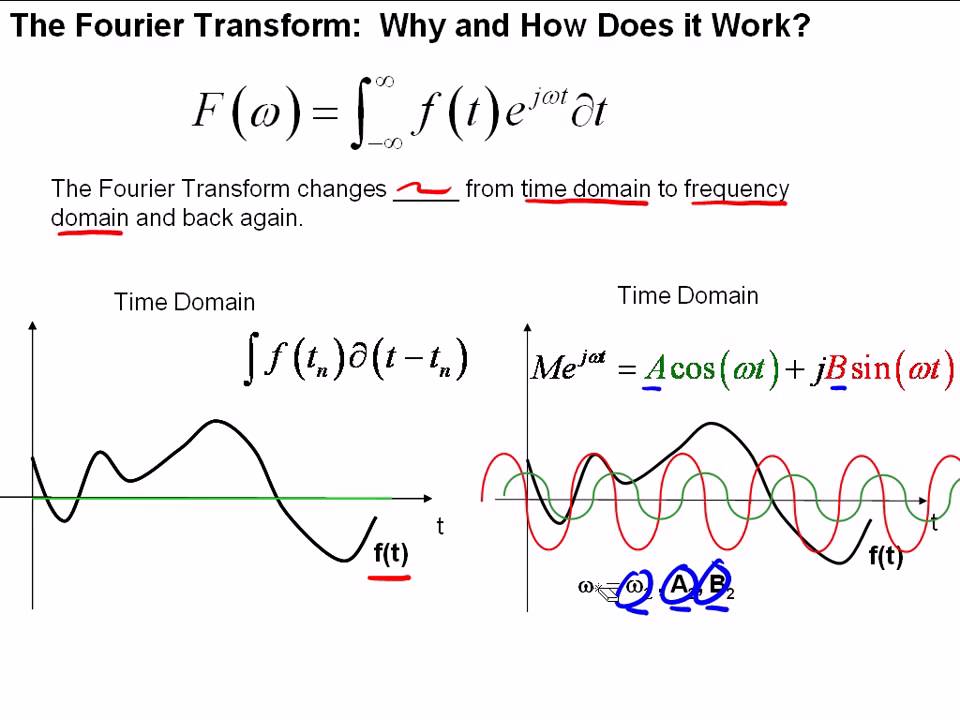
The Fourier Transform Part I Youtube The output of the transform is a complex valued function of frequency. the term fourier transform refers to both this complex valued function and the mathematical operation. when a distinction needs to be made, the output of the operation is sometimes called the frequency domain representation of the original function. The above function is for continuous functions, for discrete functions we use discrete fourier transform. applications. the fourier transform gives you answer questions about a sound that is. Wait! we need to offset each spike with a phase delay (the angle for a "1 second delay" depends on the frequency). actual recipe for a frequency = a 4 (no offset) b 4 (1 second offset) c 4 (2 second offset) d 4 (3 second offset). we can then loop through every frequency to get the full transform. We saw in our discussion of the continuous fourier transform of a sine function that evaluating the integrals in software gave very small extraneous values for the real parts of the transform. this is also an issue for the discrete fourier transform, but is compounded by the fact that the signal is sampled and not continuous.
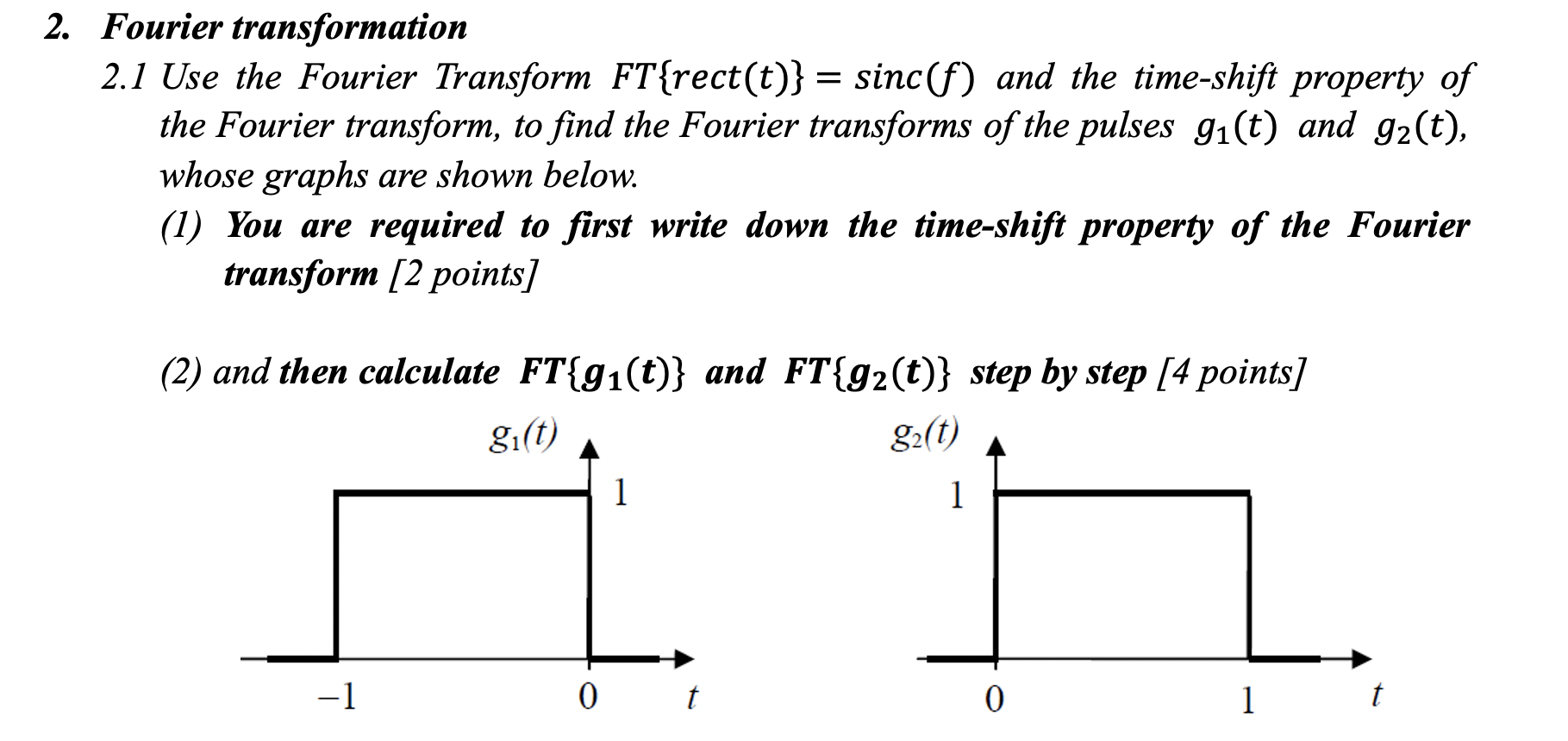
2 Fourier Transformation 21 Use The Fourier Transform Ftrecttsincf And Wait! we need to offset each spike with a phase delay (the angle for a "1 second delay" depends on the frequency). actual recipe for a frequency = a 4 (no offset) b 4 (1 second offset) c 4 (2 second offset) d 4 (3 second offset). we can then loop through every frequency to get the full transform. We saw in our discussion of the continuous fourier transform of a sine function that evaluating the integrals in software gave very small extraneous values for the real parts of the transform. this is also an issue for the discrete fourier transform, but is compounded by the fact that the signal is sampled and not continuous. The fourier transform reveals a signal’s elemental periodicity by decomposing the signal into its constituent sinusoidal frequencies and identifying the magnitudes and phases of these constituent frequencies. the word “decomposing” is crucial here. the fourier transform teaches us to think about a time domain signal as a waveform that is. 9 fourier transform properties. the fourier transform is a major cornerstone in the analysis and representa tion of signals and linear, time invariant systems, and its elegance and impor tance cannot be overemphasized. much of its usefulness stems directly from the properties of the fourier transform, which we discuss for the continuous time.

Comments are closed.