Vertex Form Of Quadratic Functions The Basics Algebra 1 Lesson

Vertex Form Of Quadratic Functions The Basics Algebra 1 Lesson Join me as i show you how to find the vertex, axis of symmetry, and whether a parabola is facing up or down from vertex from of a quadratic. my name is laur. Quadratic functions & equations: unit test our mission is to provide a free, world class education to anyone, anywhere. khan academy is a 501(c)(3) nonprofit organization.

Algebra 1 Graphing Quadratic Functions In Vertex Form Youtube Course: algebra 1 > unit 14. lesson 4: vertex form. vertex form introduction. graphing quadratics: vertex form. graph quadratics in vertex form. quadratic word problems (vertex form) quadratic word problems (vertex form). To convert from f (x) = ax2 bx c form to vertex form: method 1: completing the square. to convert a quadratic from y = ax2 bx c form to vertex form, y = a (x h) 2 k, you use the process of completing the square. let's see an example. convert y = 2x2 4x 5 into vertex form, and state the vertex. equation in y = ax2 bx c form. Unit 8 – quadratic functions and their algebra. these lessons introduce quadratic polynomials from a basic perspective. we then build on the notion of shifting basic parabolas into their vertex form. completing the square is used as a fundamental tool in finding the turning point of a parabola. finally, the zero product law is introduced as a. The equation for a basic parabola with a vertex at (0, 0) is y = x 2. you can apply transformations to the graph of y = x 2 to create a new graph with a corresponding new equation. this new equation can be written in vertex form. the vertex form of a quadratic function is y = a (x − h) 2 k where: | a | is the vertical stretch factor.

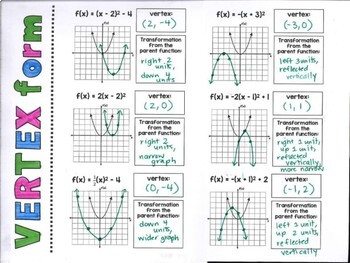
Algebra 1 Transformations Of Quadratic Functions Vertex Form Foldable Unit 8 – quadratic functions and their algebra. these lessons introduce quadratic polynomials from a basic perspective. we then build on the notion of shifting basic parabolas into their vertex form. completing the square is used as a fundamental tool in finding the turning point of a parabola. finally, the zero product law is introduced as a. The equation for a basic parabola with a vertex at (0, 0) is y = x 2. you can apply transformations to the graph of y = x 2 to create a new graph with a corresponding new equation. this new equation can be written in vertex form. the vertex form of a quadratic function is y = a (x − h) 2 k where: | a | is the vertical stretch factor. Activity 1: vertical stretches example 1 1. given below are three quadratic functions of the form y = a x 2. complete the tables for each, and graph each on the same axes. find the differences between consecutive values in the tables. represent this on the graphs of each with example slope triangles. what do these differences and slope. The vertex form of a quadratic function is y = a(x − h)2 k where: | a | is the vertical stretch factor. if a is negative, there is a vertical reflection and the parabola will open downwards. k is the vertical translation. h is the horizontal translation. given the equation of a parabola in vertex form, you should be able to sketch its graph.