Use Reference Angles To Evaluate Trig Functions

Lesson 73 Reference Angles Using Reference Angles To Evaluate Reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. they can also be used to find [latex]\left(x,y\right)[ latex] coordinates for those angles. we will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the angle lies. This trigonometry video tutorial explains how to use reference angles to evaluate trigonometric functions such as sine, cosine, tangent, secant, cosecant, an.
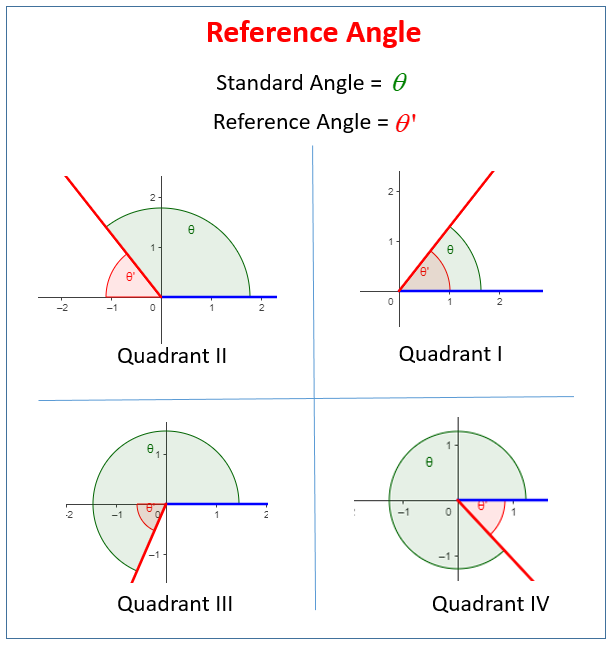
Evaluating Trigonometric Functions Using The Reference Angle Solutions To find the value of a trigonometric function of any angle t: determine the function value for the associated reference angle t'. depending on the quadrant in which t lies, the answer will be either be or . how to evaluate trig functions using reference angles? find the reference angle for the given angle. Using reference angles. reference angles make it possible to evaluate trigonometric functions for angles outside the first quadrant. they can also be used to find [latex]\left(x,y\right)[ latex] coordinates for those angles. we will use the reference angle of the angle of rotation combined with the quadrant in which the terminal side of the. Evaluating trigonometric functions using reference angles. we can use reference angles to help us evaluate a trigonometric function at a non acute angle \( \theta \). to do so, we construct a reference triangle for \( \theta \) using the following method: choose a point \(p\) on the terminal side of \( \theta \). Reference angle. 9. 2 3s j the angle j is on the positive y axis. thus, the angle j does not have a reference angle. back to topics list 2. the reference angle of the special angles the reference angle of the special angles of , 6 7, 6 5, 6 s s s r r r and 11s r is 6 s. the reference angle of the special angles of , 4 5, 4 3, 4 s s s r r r and.

Evaluating Trig Functions Using Reference Angles Youtube Evaluating trigonometric functions using reference angles. we can use reference angles to help us evaluate a trigonometric function at a non acute angle \( \theta \). to do so, we construct a reference triangle for \( \theta \) using the following method: choose a point \(p\) on the terminal side of \( \theta \). Reference angle. 9. 2 3s j the angle j is on the positive y axis. thus, the angle j does not have a reference angle. back to topics list 2. the reference angle of the special angles the reference angle of the special angles of , 6 7, 6 5, 6 s s s r r r and 11s r is 6 s. the reference angle of the special angles of , 4 5, 4 3, 4 s s s r r r and. Related to , called the reference angle of . de nition 2.1. the reference angle of a non square angle is the acute angle formed between the x axis and the ray from the origin making an angle of with the positive x axis ray. recall that the xy plane is traditionally divided into four quadrants, hence dividing the non square angles in one. Reference angles, by definition, always have a measure between 0 and . due to the periodic nature of the trigonometric functions, the value of a trigonometric function at a given angle is always the same as its value at that angle's reference angle, except when there is a variation in sign. because we know the signs of the functions in.

How To Use Reference Angles To Evaluate Trigonometric Functions Youtube Related to , called the reference angle of . de nition 2.1. the reference angle of a non square angle is the acute angle formed between the x axis and the ray from the origin making an angle of with the positive x axis ray. recall that the xy plane is traditionally divided into four quadrants, hence dividing the non square angles in one. Reference angles, by definition, always have a measure between 0 and . due to the periodic nature of the trigonometric functions, the value of a trigonometric function at a given angle is always the same as its value at that angle's reference angle, except when there is a variation in sign. because we know the signs of the functions in.

Use Reference Angles To Evaluate Trig Functions Supermath4u Youtube
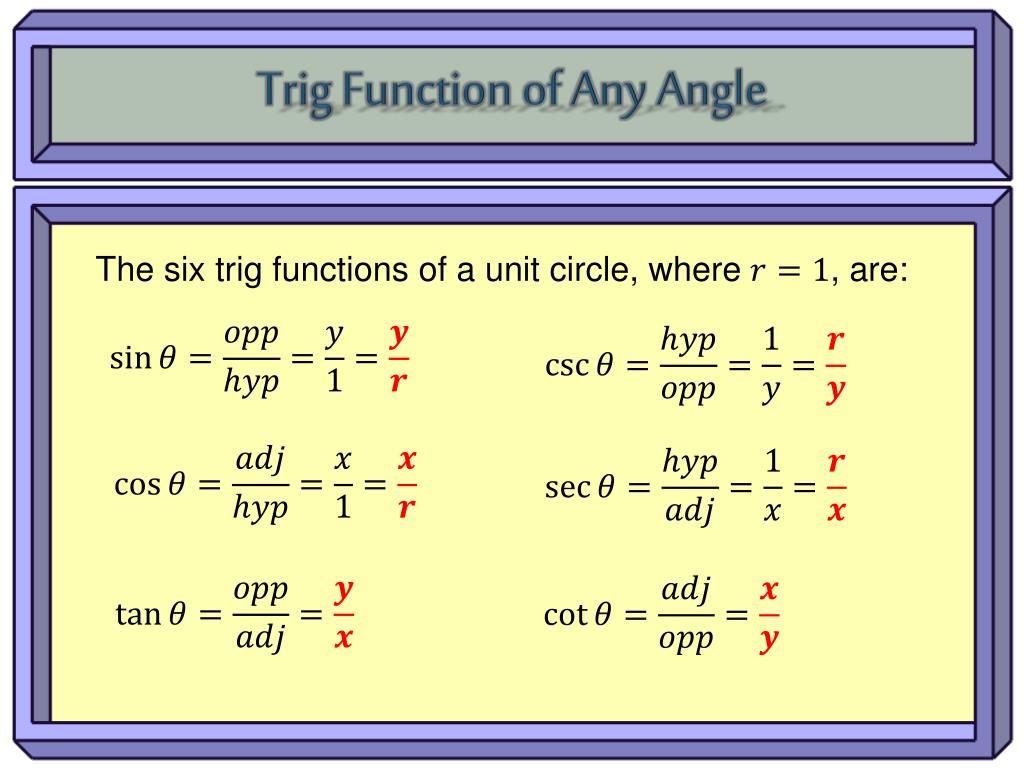
Ppt Trigonometric Functions Powerpoint Presentation Free Download

Comments are closed.