Understanding The Fourier Transform By Example Ritchie Vink

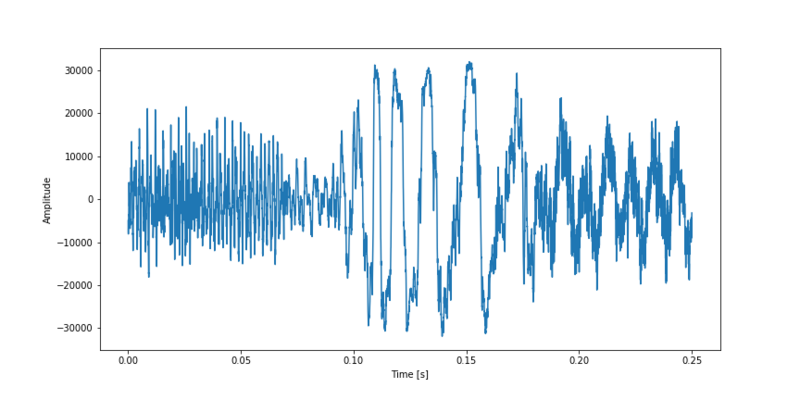
Understanding The Fourier Transform By Example Ritchie Vink The fourier transform is commonly used to convert a signal in the time spectrum to a frequency spectrum. examples of time spectra are sound waves, electricity, mechanical vibrations etc. the figure below shows 0,25 seconds of kendrick’s tune. as can clearly be seen it looks like a wave with different frequencies. Understanding the fourier transform by example 23 04 2017 ; writing a fourth order runga kutta solver for a vibrations problem in python 2020 ritchie vink.

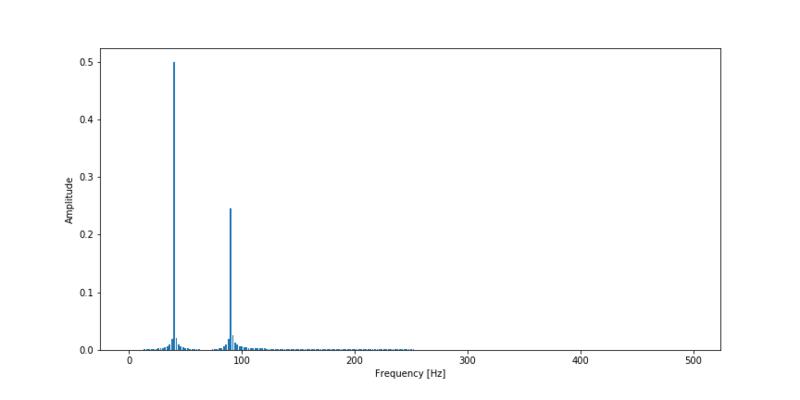
Understanding The Fourier Transform By Example Ritchie Vink In the last couple of weeks i have been playing with the results of the fourier transform and it has quite some interesting properties that initially were not clear to me. in this post i summarize the things i found interesting and the things i’ve learned about the fourier transform. Wait! we need to offset each spike with a phase delay (the angle for a "1 second delay" depends on the frequency). actual recipe for a frequency = a 4 (no offset) b 4 (1 second offset) c 4 (2 second offset) d 4 (3 second offset). we can then loop through every frequency to get the full transform. Thereby inverse fourier transform is given by similarly if fourier sine transform is taken as , then inverse sine transform is given by similar is the case with fourier cosine transform. example 1 state giving reasons whether the fourier transforms of the following functions exist: i. ii. iii. solution: i. the graph of. The fourier transform of an intensity vs. time function, like g (t) g(t), is a new function, which doesn't have time as an input, but instead takes in a frequency, what i've been calling "the winding frequency." in terms of notation, by the way, the common convention is to call this new function \hat g (f) g^(f) with a little circumflex on top.

Understanding The Fourier Transform By Example Ritchie Vink Thereby inverse fourier transform is given by similarly if fourier sine transform is taken as , then inverse sine transform is given by similar is the case with fourier cosine transform. example 1 state giving reasons whether the fourier transforms of the following functions exist: i. ii. iii. solution: i. the graph of. The fourier transform of an intensity vs. time function, like g (t) g(t), is a new function, which doesn't have time as an input, but instead takes in a frequency, what i've been calling "the winding frequency." in terms of notation, by the way, the common convention is to call this new function \hat g (f) g^(f) with a little circumflex on top. Fourier transforms (with python examples) written on april 6th, 2024 by steven morse. fourier transforms are, to me, an example of a fundamental concept that has endless tutorials all over the web and textbooks, but is complex (no pun intended!) enough that the learning curve to understanding how they work can seem unnecessarily steep. Foundations of fourier transformations. the fundamental idea behind fourier transformations is that a function can be expressed as a weighted sum of periodic basis functions such as sines and cosines. in fact, the fourier transform expresses a signal as a sum of sinusoids which we call “a representation in fourier space.”.