Understanding The Derivative From A Graphical And Numerical Approach

Understanding The Derivative From A Graphical And Numerical Approach Understanding the derivative from a graphical and numerical approach so far, our understanding of the derivative is that it represents the slope of the tangent line drawn to a curve at a point. Welcome to my channel miftah math lessons!in this lesson, i explained how to find derivatives from graphs. since the derivative represents the slope of the t.

Ppt Graphical Differentiation Powerpoint Presentation Free Download 10.5 derivatives: numerical and graphical viewpoints. definition: the instantaneous rate of change of f(x) at x = a is defined as. h f a ' a lim 0hthe quantity f . (a) is also called the derivative of f(x) at x = a. findi. g the derivative is also known as differentiating f. the units of f′(a) are the same as the units of. he average rate of. Determining the graph of a derivative of a function. suppose a function is f (x)=x^3 12x 3 f (x) = x3 −12x 3 and its graph is as follows: forget the equation for a moment and just look at the graph. now, to find the graph of {f}' f ′ from the above graph, we have to find two kinds of very important points. Units of the derivative function. as we now know, the derivative of the function f at a fixed value x is given by f ′ (x) = lim h → 0f(x h) − f(x) h, and this value has several different interpretations. if we set x = a, one meaning of f ′ (a) is the slope of the tangent line at the point (a, (f(a)). in alternate notation, we also. The derivative of a function can be interpreted in different ways. it can be observed as the behavior of a graph of the function or calculated as a numerical rate of change of the function. the derivative of a function \(f(x)\) at a point \(x=a\) is the slope of the tangent line to the curve \(f(x)\) at \(x=a\).

Graphically Representing The Derivative Of A Function Calculus Units of the derivative function. as we now know, the derivative of the function f at a fixed value x is given by f ′ (x) = lim h → 0f(x h) − f(x) h, and this value has several different interpretations. if we set x = a, one meaning of f ′ (a) is the slope of the tangent line at the point (a, (f(a)). in alternate notation, we also. The derivative of a function can be interpreted in different ways. it can be observed as the behavior of a graph of the function or calculated as a numerical rate of change of the function. the derivative of a function \(f(x)\) at a point \(x=a\) is the slope of the tangent line to the curve \(f(x)\) at \(x=a\). Example 44: understanding the graph of the derivative. consider the graph of f(x) and its derivative, f′(x), in figure 2.12 (a). use these graphs to find the slopes of the tangent lines to the graph of f at x = 1, x = 2, and x = 3. figure 2.12: graphs of f and f′ in example 44, along with tangent lines in (b). solution. Mth 132 chapter 2 derivatives msu 2.3video a graphical viewpoint objective(s): given a graph of a function sketch the graph of its derivative. as we saw at the beginning of this section computers are quite good at graphing the derivative function given the original function. we would like to gain this skill as well.

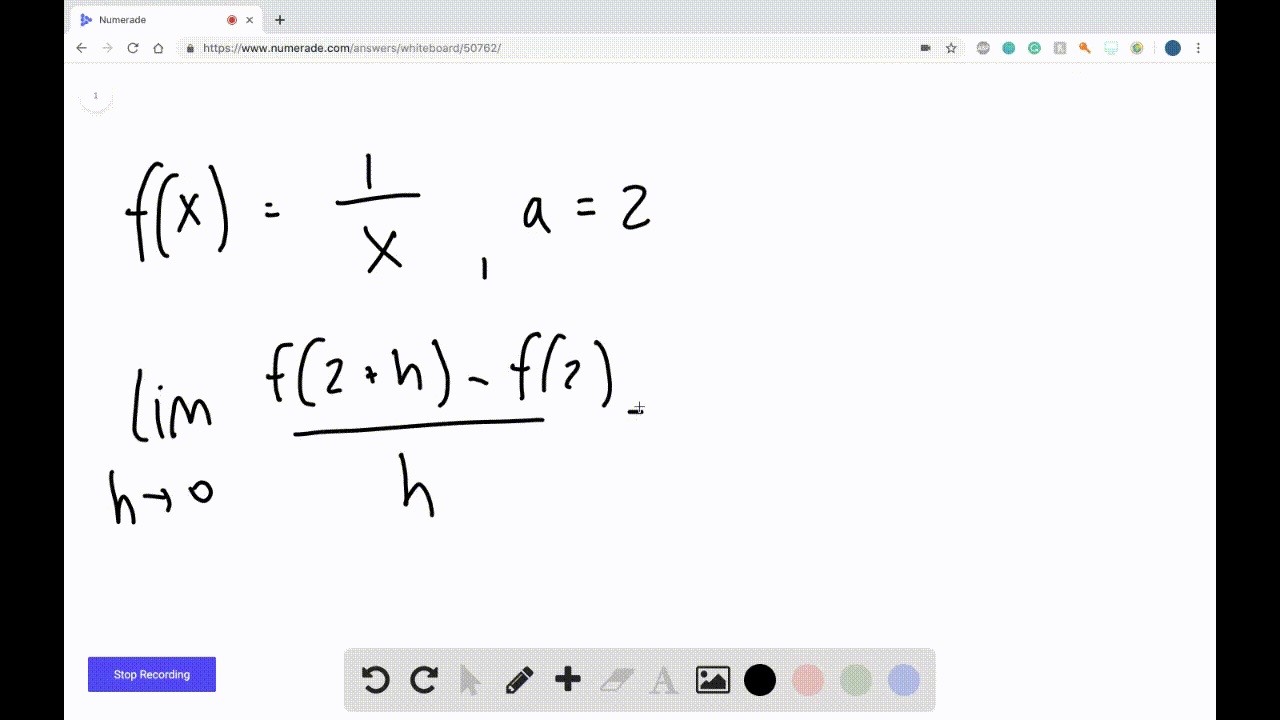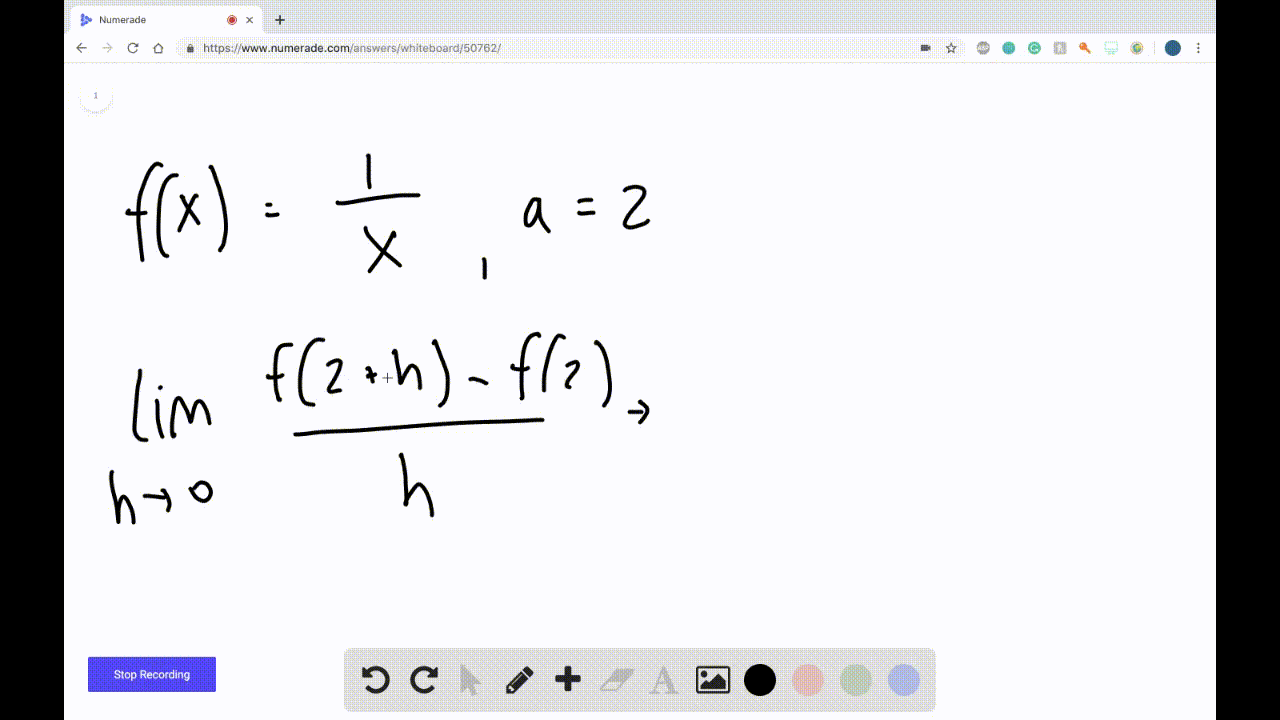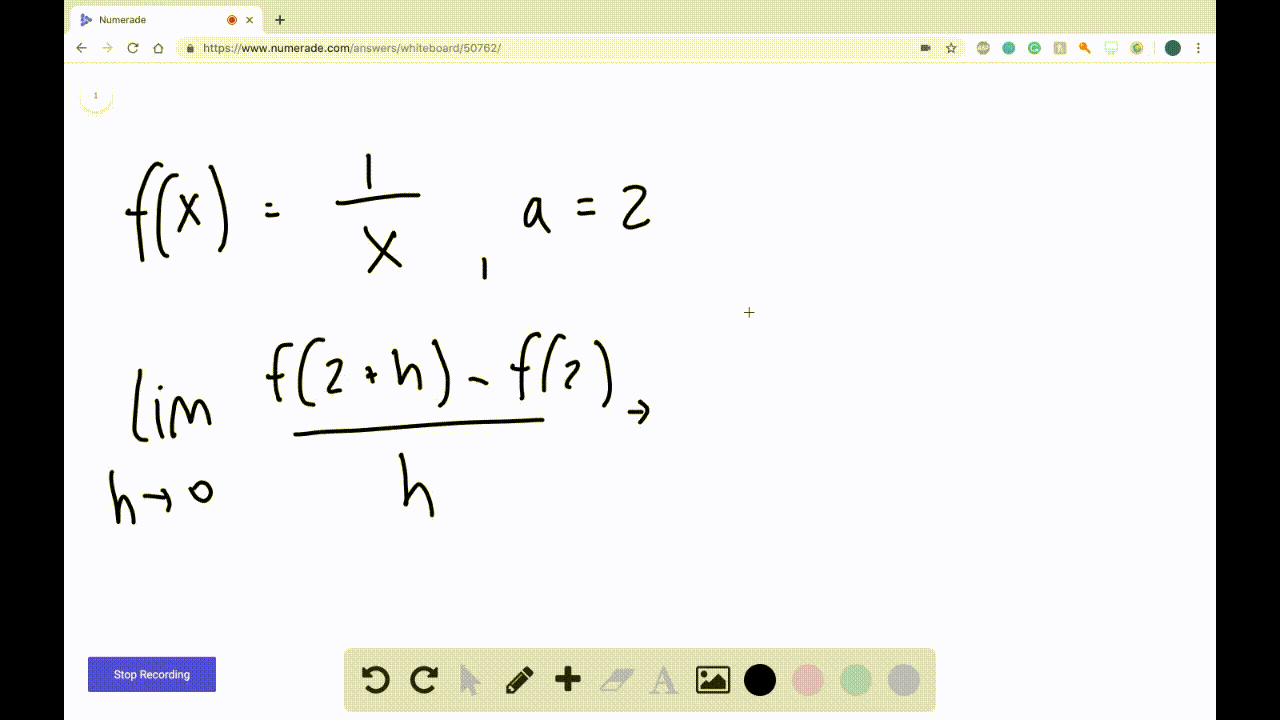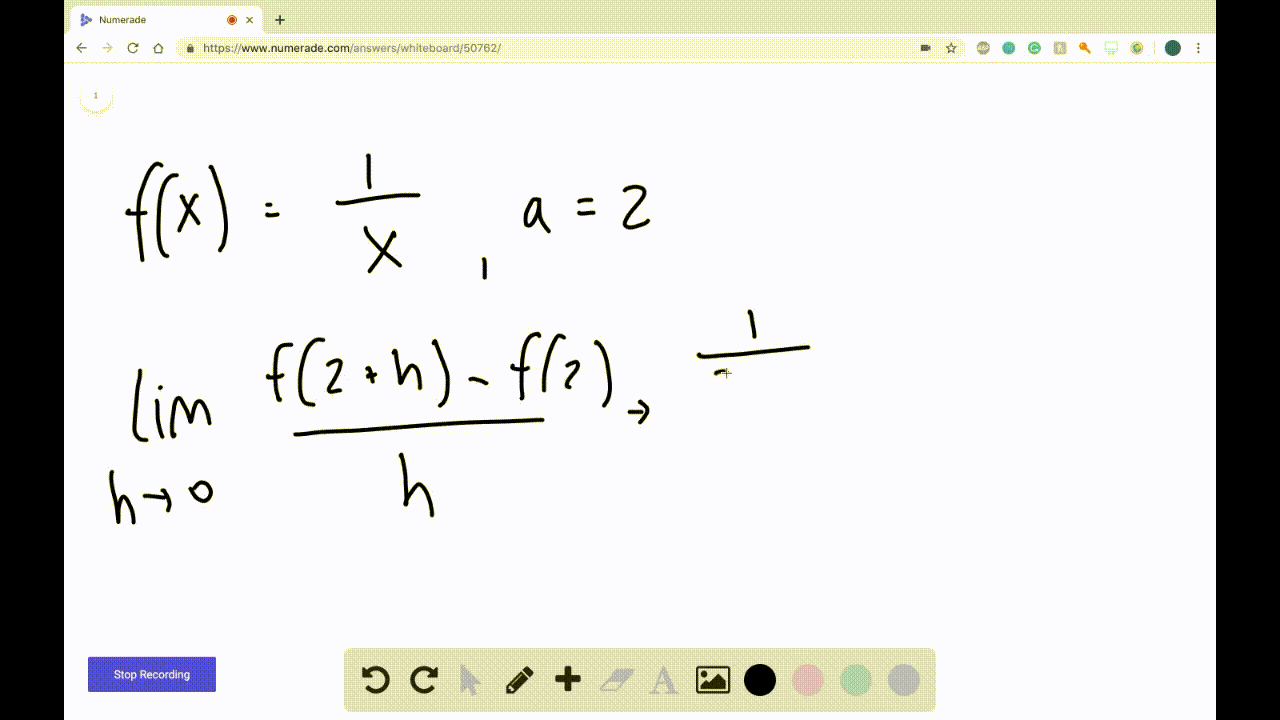
Derivatives Calculus Graphical Numerical Alg Example 44: understanding the graph of the derivative. consider the graph of f(x) and its derivative, f′(x), in figure 2.12 (a). use these graphs to find the slopes of the tangent lines to the graph of f at x = 1, x = 2, and x = 3. figure 2.12: graphs of f and f′ in example 44, along with tangent lines in (b). solution. Mth 132 chapter 2 derivatives msu 2.3video a graphical viewpoint objective(s): given a graph of a function sketch the graph of its derivative. as we saw at the beginning of this section computers are quite good at graphing the derivative function given the original function. we would like to gain this skill as well.

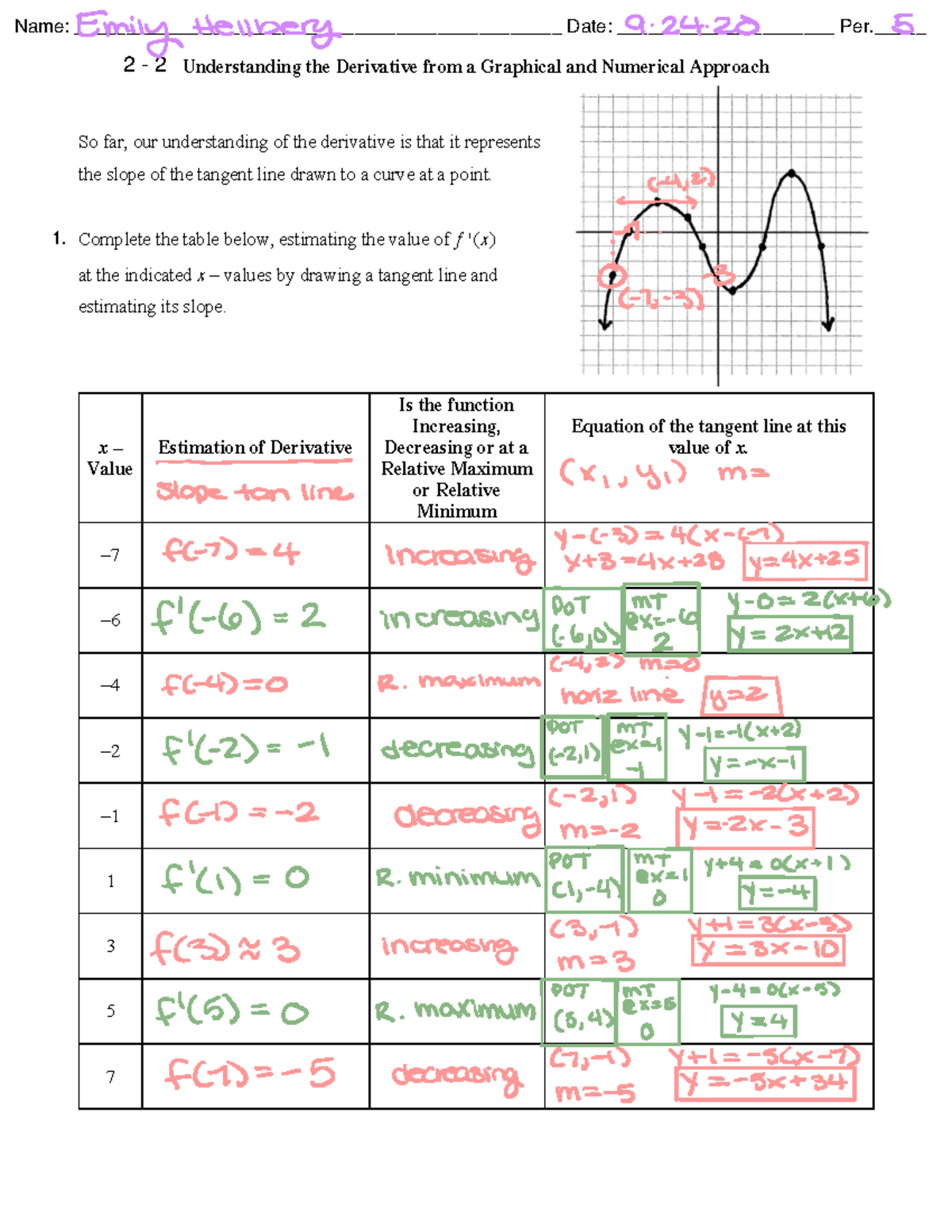
2 2 Derivative Graphically And Numerically Understanding The