Ultimate Guide To Gmat Geometry Part Ii Perimeter Area Parallelograms Chapter 6: gmat geometry does perimeter and area. the perimeter of an object is described as the sum of the length of its sides. in other words, find a way to get the length of all the sides, add them up, and that’s your perimeter. The base of the parallelogram is 1087m and the height is 8m. what is the base of the parallelogram rounded to the nearest tenth? 187. find the area of the parallelogram. 500. find the area of the parallelogram. 243. find the area of the parallelogram. 3,750.
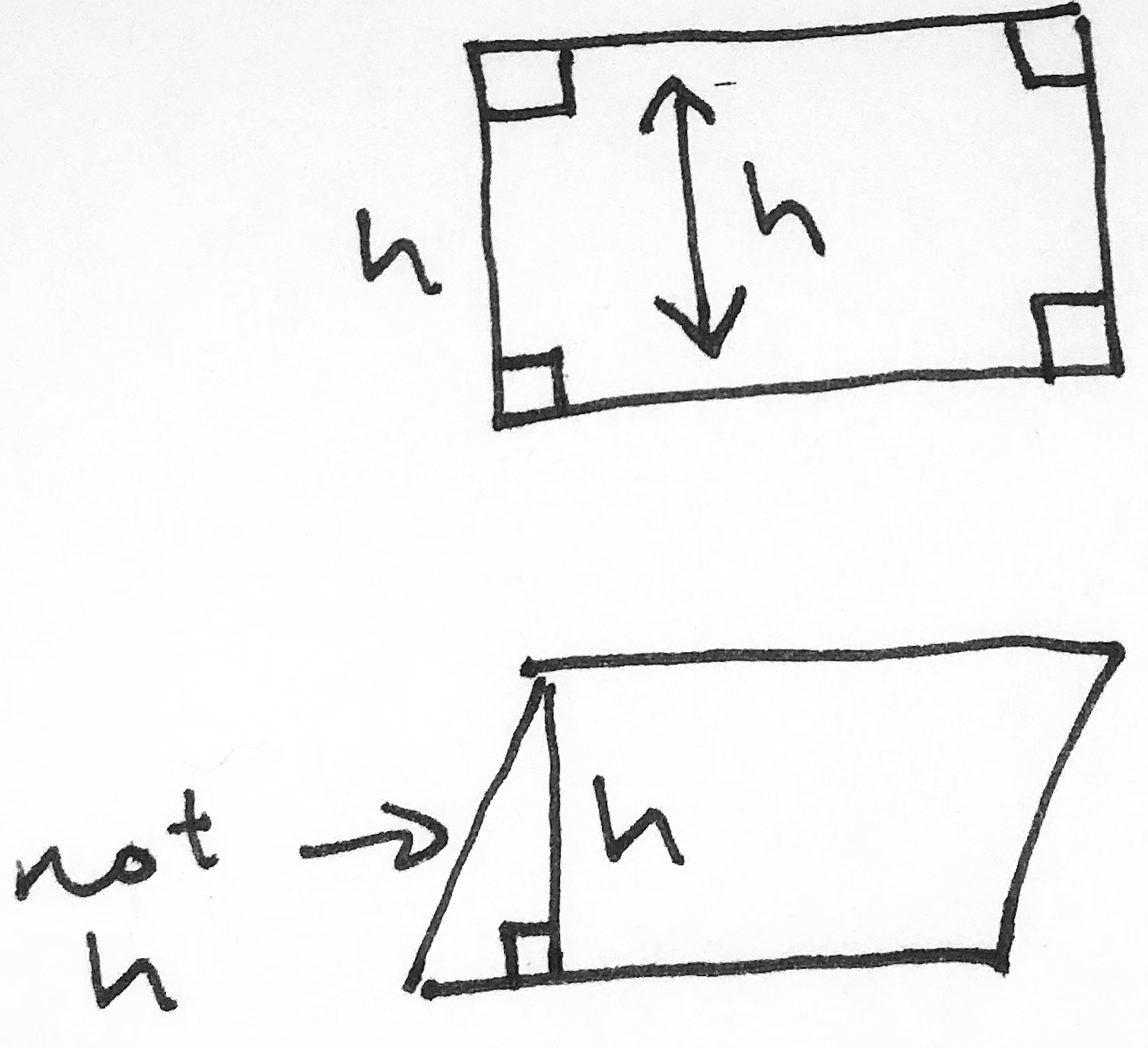
Ultimate Guide To Gmat Geometry Part Ii Perimeter Area Parallelograms See the attached figure. all 3 parallelogram have area 35, as height is 5 in each case. we can have infinite solutions. insufficient. (2) wx xy is 12. sum of adjacent sides is 12, so perimeter =2*12=24. sufficient. The gmat the definitive shortcuts guide is not only just a collection of simple tricks or shortcuts for the quantitative reasoning portion of the gmat. i strongly recommend studying for a more complete and robust quant theory knowledge for the gmat. number system shortcuts algebra shortcuts geometry shortcuts 1. method to multiply 2 digit number. Now, all we have to do is plug these numbers into our formula: a = bh = (12)(6) = 72 cm2 a = b h = (12) (6) = 72 cm 2. we need to be sure that we have our units right. for area, the units are always squared, while for perimeter they are not. the area of our parallelogram is 72 cm2 72 cm 2, or 72 square centimeters. We can calculate the area of a parallelogram when we know the lengths of the diagonals and the angle of intersection of the diagonals. then, we use the following formula: a=\frac {d {1}\times d {2}\sin (y)} {2} a = 2d1×d2 sin(y) where, d {1}, ~d {2} d1, d2 are the lengths of the diagonals and y is the angle of intersection of the diagonals.
Ultimate Guide To Gmat Geometry Part Ii Perimeter Area Parallelograms Now, all we have to do is plug these numbers into our formula: a = bh = (12)(6) = 72 cm2 a = b h = (12) (6) = 72 cm 2. we need to be sure that we have our units right. for area, the units are always squared, while for perimeter they are not. the area of our parallelogram is 72 cm2 72 cm 2, or 72 square centimeters. We can calculate the area of a parallelogram when we know the lengths of the diagonals and the angle of intersection of the diagonals. then, we use the following formula: a=\frac {d {1}\times d {2}\sin (y)} {2} a = 2d1×d2 sin(y) where, d {1}, ~d {2} d1, d2 are the lengths of the diagonals and y is the angle of intersection of the diagonals. Gmat geometry syllabus covers 10 to 15% of the gmat quant portion. this means you could get 3 to 6 questions out of 31 questions on exam day. the gmat geometry syllabus mostly focuses on triangles, quadrilaterals, and straight lines, although parabolas in coordinate geometry are occasionally tested. angles, side, area, and perimeter are often. Find the area of the parallelogram. you find the area of the parallelogram by using the formula above: a = 4 cm ⋅ 5 cm = 2 0 cm 2. learn how to compute the perimeter and area of a parallelogram. the formula for the area of a parallelogram is "base times width". discover more here!.
Comments are closed.