Types Of Angles Vertical Corresponding Alternate Interior Others
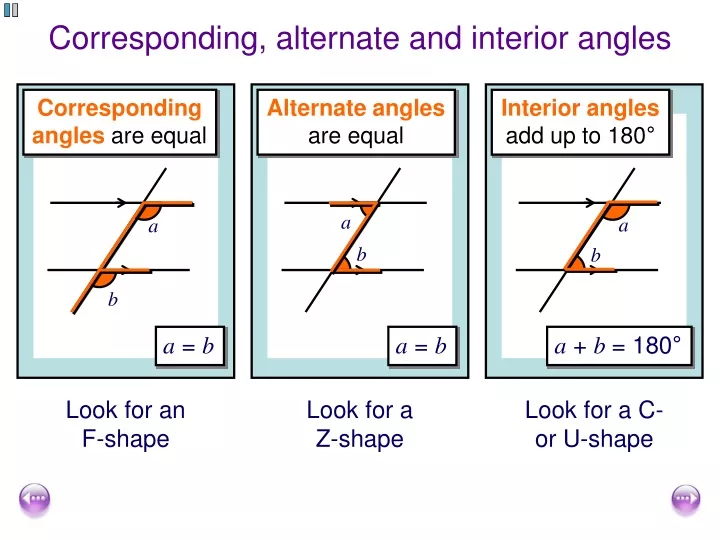
Ppt Corresponding Alternate And Interior Angles Powerpoint Types of angles. in geometry, there are many types of angles such as congruent, adjacent, vertical, corresponding, alternating, exterior, and interior angles. all angles have relationships to other angles and those angle relationships are what we will cover here. get free estimates from geometry tutors near you. An angle is defined as the amount of turn between two lines, segments, or rays. some angles are well known. for example, to turn a corner is usually 90 degrees. the corners of a piece of paper are.

Interior Alternate Vertically Opposite And Corresponding Angle Alternate interior angles are formed when a transversal crosses two parallel or non parallel lines. one way to help you identify this angle pair is to look closely at the words alternate and interior. in our diagram above, both are located on the inner side or in between the lines . they are also on opposite sides of the transversal and are not. Alternate interior angles. when two lines are crossed by another line (called the transversal): alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. in this example c and f are a pair of alternate interior angles. also d and e are a pair of alternate interior. Alternate interior angles examples. example 1: find the measure of angle x in the following figure if the two lines are parallel and they are crossed by a transversal. solution: by the alternate interior angles theorem, x and 20° are the alternate interior angles. hence, they are equal. Corresponding angles are equal to each other. one way to find the corresponding angles is to draw a letter f on the diagram. the f can also be facing backwards. in the above diagram, ∠d and ∠h are corresponding angles. there many other corresponding pairs of angles in the diagram: ∠b and ∠f; ∠c and ∠g; ∠a and ∠e.
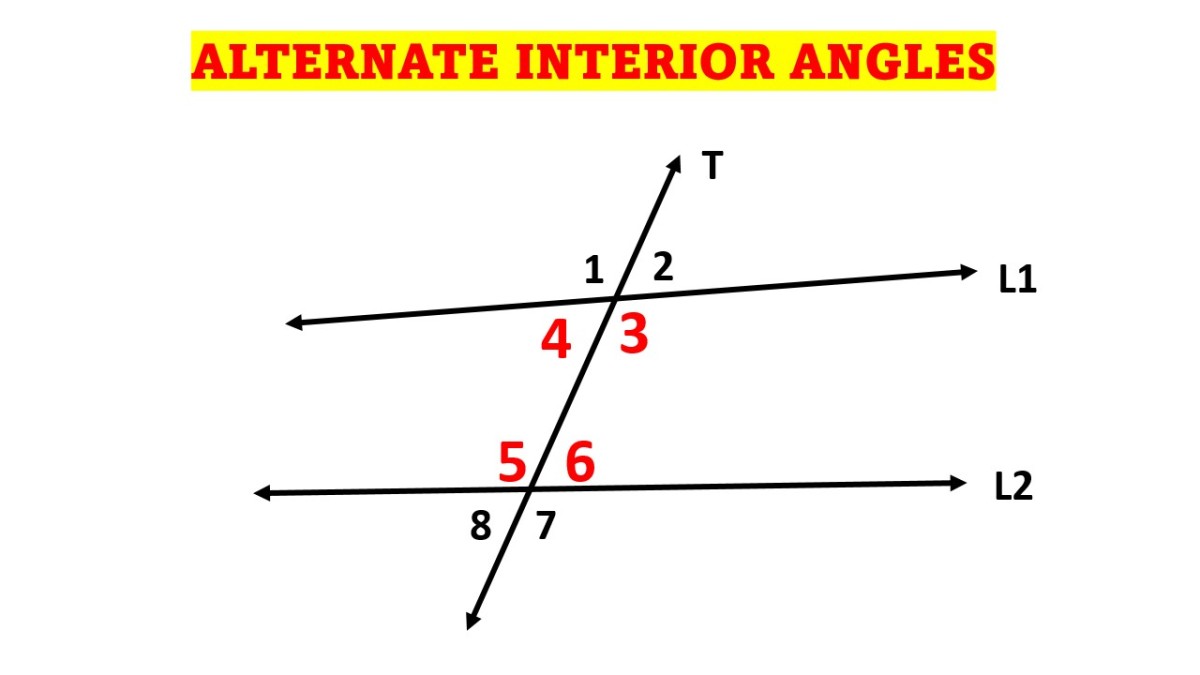
Alternate Interior Angles Examples Definition Theorem Education Tips Alternate interior angles examples. example 1: find the measure of angle x in the following figure if the two lines are parallel and they are crossed by a transversal. solution: by the alternate interior angles theorem, x and 20° are the alternate interior angles. hence, they are equal. Corresponding angles are equal to each other. one way to find the corresponding angles is to draw a letter f on the diagram. the f can also be facing backwards. in the above diagram, ∠d and ∠h are corresponding angles. there many other corresponding pairs of angles in the diagram: ∠b and ∠f; ∠c and ∠g; ∠a and ∠e. Example 2: find pairs of corresponding angles. ← s→ y s y and ← t → z t z are parallel lines. name all pairs of corresponding angles. identify two parallel lines that are intersected by a transversal. show step. the two parallel lines are sy s y and t z. tz. line u x u x is the transversal. 1. use the alternate interior angles theorem to determine if the lines cut by the transversal are parallel. solution: angle a and the angle measuring 60 ∘ form a straight angle. thus, m ∠ a 60 ∘ = 180 ∘. m ∠ a = 120 ∘. similarly, ∠ b and 120 ∘ form a straight angle, so we know that. m ∠ b 120 = 180. m ∠ b = 60 ∘.
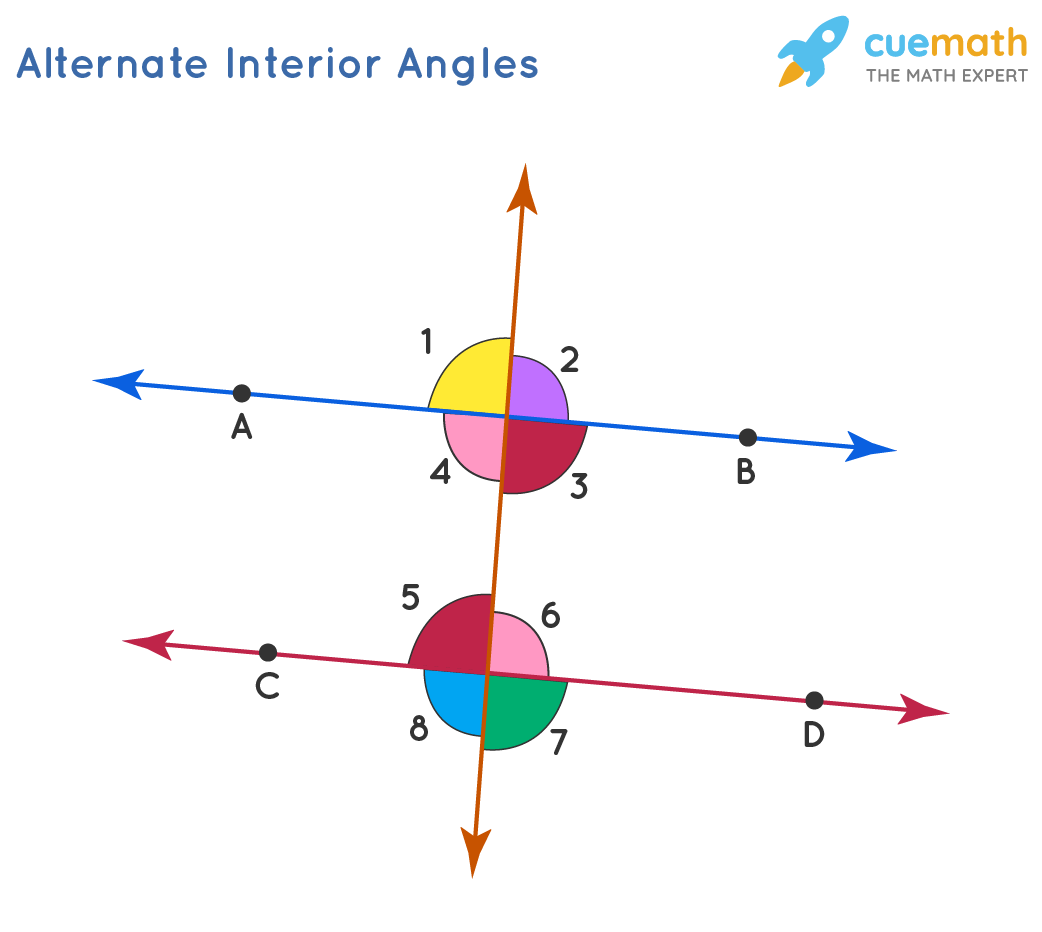
Alternate Interior Angles Definition Theorems Examples Example 2: find pairs of corresponding angles. ← s→ y s y and ← t → z t z are parallel lines. name all pairs of corresponding angles. identify two parallel lines that are intersected by a transversal. show step. the two parallel lines are sy s y and t z. tz. line u x u x is the transversal. 1. use the alternate interior angles theorem to determine if the lines cut by the transversal are parallel. solution: angle a and the angle measuring 60 ∘ form a straight angle. thus, m ∠ a 60 ∘ = 180 ∘. m ∠ a = 120 ∘. similarly, ∠ b and 120 ∘ form a straight angle, so we know that. m ∠ b 120 = 180. m ∠ b = 60 ∘.

Angles Rules In Parallel Lines Alternate Co Interior Corresponding

Comments are closed.