Types Of Angles And Angle Relationships
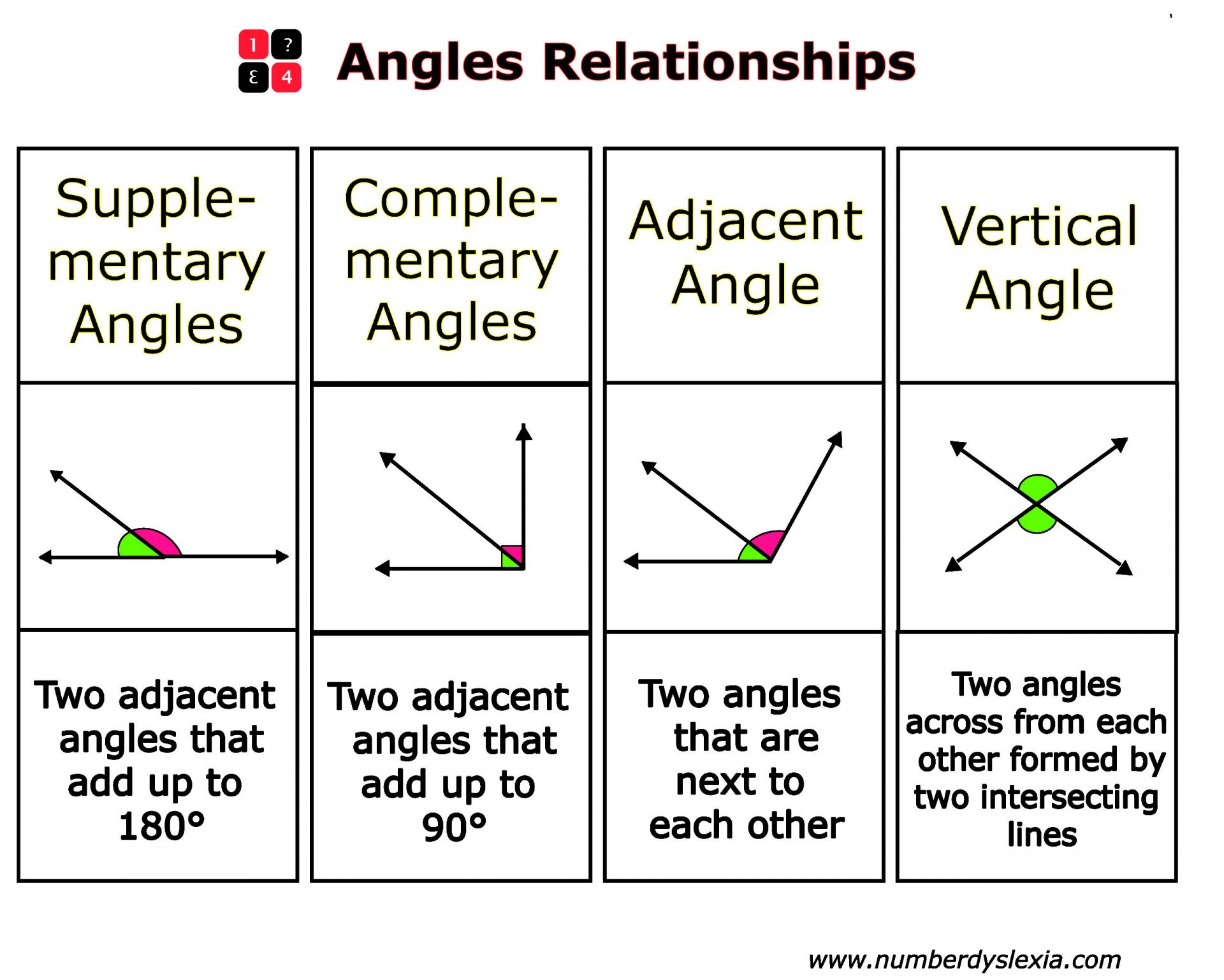
Types Of Angles Chart Types of angles. in geometry, there are many types of angles such as congruent, adjacent, vertical, corresponding, alternating, exterior, and interior angles. all angles have relationships to other angles and those angle relationships are what we will cover here. get free estimates from geometry tutors near you. Adjacent angles examples. and as math is fun so nicely points out, a straightforward way to remember complementary and supplementary measures is to think: c is for corner of a right angle (90 degrees) s is for straight angle (180 degrees) now it’s time to talk about my two favorite angle pair relationships: linear pair and vertical angles.

Types Of Angles In Geometry What are angles? what kinds of angles are there and how do they relate? vertical angles, supplementary angles, complementary angles, corresponding angles, we. Let us see the above different types of angle relationships in detail. (i) congruent angles : congruent angles are angles that have the same measure. (ii) vertical angles : vertical angles have a common vertex, but they are never adjacent angles. and also, vertical angles are always congruent. (iii) complementary angles :. Transversals creates three important types of angles, namely: 1. corresponding angles. 2. co interior angles. 3. alternating angles. corresponding angles are in the same position as each other. co interior angles are between the lines and on the same side of the transversal. X = 3k = 3 × 18 = 54°. y = 7k = 7 × 18 = 126°. thus, ∠x = 54° and ∠y = 126°. ∠x = ∠z = 54° (vertically opposite angles). example 2: in the following figure l1 and l2 are two perpendicular lines that intersect at o. through o, another straight line m is drawn; some angles thus formed have been marked.

8 G 5 Angle Relationships Mr Hill S Math Transversals creates three important types of angles, namely: 1. corresponding angles. 2. co interior angles. 3. alternating angles. corresponding angles are in the same position as each other. co interior angles are between the lines and on the same side of the transversal. X = 3k = 3 × 18 = 54°. y = 7k = 7 × 18 = 126°. thus, ∠x = 54° and ∠y = 126°. ∠x = ∠z = 54° (vertically opposite angles). example 2: in the following figure l1 and l2 are two perpendicular lines that intersect at o. through o, another straight line m is drawn; some angles thus formed have been marked. An angle is defined as the amount of turn between two lines, segments, or rays. some angles are well known. for example, to turn a corner is usually 90 degrees. the corners of a piece of paper are. Example 1: given the diagram below, determine the values of the angles x, y and z. solution: step 1: x is a supplement of 65°. therefore, x 65° = 180° ⇒ x = 180° – 65° = 115°. step 2: z and 115° are vertical angles. therefore, z = 115°. step 3: y and 65° are vertical angles. therefore, y = 65°.

Angle Relationships An angle is defined as the amount of turn between two lines, segments, or rays. some angles are well known. for example, to turn a corner is usually 90 degrees. the corners of a piece of paper are. Example 1: given the diagram below, determine the values of the angles x, y and z. solution: step 1: x is a supplement of 65°. therefore, x 65° = 180° ⇒ x = 180° – 65° = 115°. step 2: z and 115° are vertical angles. therefore, z = 115°. step 3: y and 65° are vertical angles. therefore, y = 65°.

Types Of Angles And Angle Relationships Youtube

Comments are closed.