Two Circles Touch Each Other Internally Prove That The Knowledgeboat Let two circles touch each other at point p and t is a point on common tangent as shown in the figure below: as tangents drawn from an external point to a circle are equal in length. from t, ta and tp are tangents to the circle with centre o'. If two tangents are drawn to a circle from an exterior point, the tangents are equal in length. let q be the point on the common tangent from which, two tangents qa and qp are drawn to the circle with centre o.
If Two Circles Touch Each Other Externally Or Internally Then The Two Two circles touch each other internally at a point p. a chord ab of the bigger circle intersects the other circle in c and d. prove that : ∠cpa = ∠dpb. To prove that the lengths of tangents drawn from any point on the common tangent to two internally touching circles are equal, we can follow these structured steps: 1 let the two circles be denoted as circle 1 with center c 1 c {1} c 1 and circle 2 with center c 2 c {2} c 2 . Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. If two given circles are touching each other internally, use this example to understand the concept of internally toucheing circles. consider the given circles. x2 y2 2x– 8 = 0 – – – (i) x 2 y 2 2 x – 8 = 0 – – – (i) and x2 y2– 6x 6y– 46 = 0 – – – (ii) x 2 y 2 – 6 x 6 y – 46 = 0 – – – (ii) let.
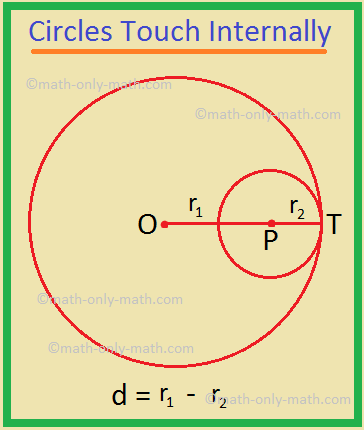
11 Two Circles Touch Each Other Internally Prove That The Tangents Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. If two given circles are touching each other internally, use this example to understand the concept of internally toucheing circles. consider the given circles. x2 y2 2x– 8 = 0 – – – (i) x 2 y 2 2 x – 8 = 0 – – – (i) and x2 y2– 6x 6y– 46 = 0 – – – (ii) x 2 y 2 – 6 x 6 y – 46 = 0 – – – (ii) let. Radii of two circles are 6.3 cm and 3.6 cm. state the distance between their centres if: they touch each other externally, they touch each other internally. in the given figure, two circles touch each other externally at point p. ab is the direct common tangent of these circles. prove that: (ii) angles apb = 90°. Two circles touch each other internally at point a as shown in the figure: ( i.sstatic js6oo ) o is the centre of bigger circle. if cb = 9 cm and de = 5.
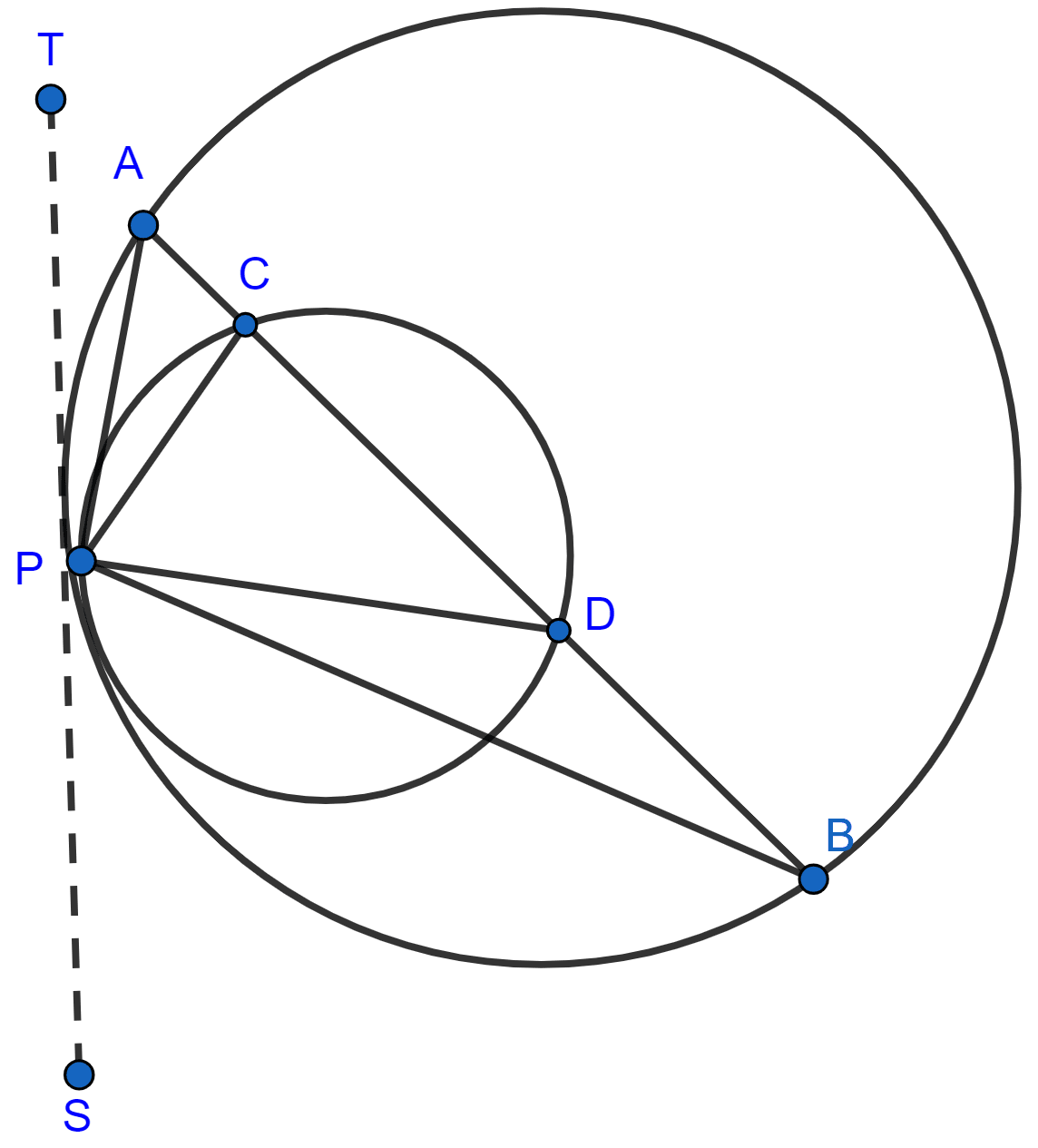
Two Circles Touch Each Other Internally At A Point P A Knowledgeboat Radii of two circles are 6.3 cm and 3.6 cm. state the distance between their centres if: they touch each other externally, they touch each other internally. in the given figure, two circles touch each other externally at point p. ab is the direct common tangent of these circles. prove that: (ii) angles apb = 90°. Two circles touch each other internally at point a as shown in the figure: ( i.sstatic js6oo ) o is the centre of bigger circle. if cb = 9 cm and de = 5.
Two Circles Touch Each Other Common Tangent Tangent Of A Circle
Two Circles Touch Each Other Internally Show That The Knowledgeboat
Comments are closed.