Two Circles Of Radius 5 And 8cm Touch Each Other Externally Mathskey
Two Circles Of Radius 5 And 8cm Touch Each Other Externally Mathskey First circle radius a = 5 cm. second circle radius b = 8 cm. the circles touch each other externally as shown in figure. length of common tangent ab can be found using the formula 2√(ab). Two circles of radius are externally tangent to each other and are internally tangent to a circle of radius at points and , as shown in the diagram. the distance can be written in the form , where and are relatively prime positive integers. what is ? solution. let the center of the surrounding circle be .
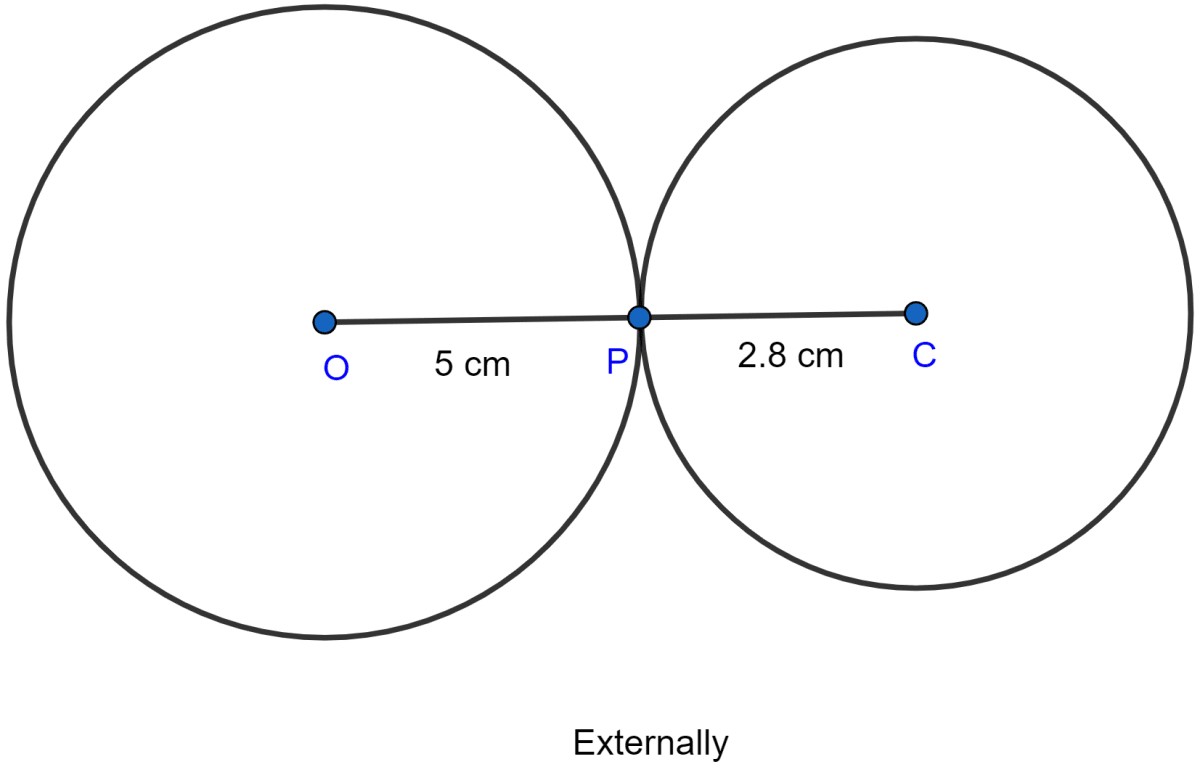
Two Circles Of Radii 5 Cm And 2 8 Cm Touch Each Other Find Knowledgeboat Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. Now adding the radius of both the given circles, we have. r1 r2 = 3 2 = 5 r 1 r 2 = 3 2 = 5. this shows that the distance between the centers of the given circles is equal to the sum of their radii. this is only possible if the circles touche each other externally, as shown in the figure. two circles touching internally equation of a. It is given that two circle having radii 3.5 cm and 4.8 cm touch each other internally. we know, the distance between the centres of the circles touching internally is equal to the difference of their radii. ∴ distance between the centres of the two circles = 4.8 cm − 3.5 cm = 1.3 cm. thus, the distance between their centres is 1.3 cm. This means that one of the angles of the parallelogram is right. therefore, based on the rectangle attribute, АОО 1 В is a rectangle. the distance between side АВ and ОО 1 is equal to the radius of the circle—that is, it is equal to r. proof of the property of the circles that touch externally. step 3.
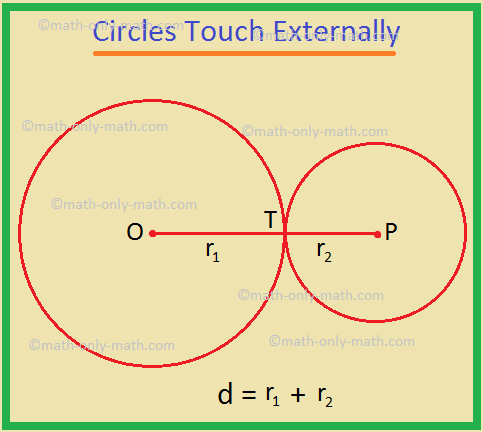
Two Circles Touch Each Other Common Tangent Tangent Of A Circle It is given that two circle having radii 3.5 cm and 4.8 cm touch each other internally. we know, the distance between the centres of the circles touching internally is equal to the difference of their radii. ∴ distance between the centres of the two circles = 4.8 cm − 3.5 cm = 1.3 cm. thus, the distance between their centres is 1.3 cm. This means that one of the angles of the parallelogram is right. therefore, based on the rectangle attribute, АОО 1 В is a rectangle. the distance between side АВ and ОО 1 is equal to the radius of the circle—that is, it is equal to r. proof of the property of the circles that touch externally. step 3. For the circles to touch, we must show that they intersect at exactly one point. we have the equations of the two circles: x2 y2 = 25 x 2 y 2 = 25. and. x2 y2 − 24x − 18y 125 = 0. x 2 y 2 − 24 x − 18 y 125 = 0. substituting the first equation into the second (or alternatively subtracting the first equation from the second) gives. Note: let two circles with centres o and p touch each other at t. let ot = r1 and pt = r2 and r1 > r2. let the distance between their centres = op = d. it is clear from the figures that. • when the circles touch externally, d = r 1 r 2. • when the circles touch internally, d = r 1 r 2. 10th grade math.
If Two Circles Touch Each Other Externally Or Internally Then The Two For the circles to touch, we must show that they intersect at exactly one point. we have the equations of the two circles: x2 y2 = 25 x 2 y 2 = 25. and. x2 y2 − 24x − 18y 125 = 0. x 2 y 2 − 24 x − 18 y 125 = 0. substituting the first equation into the second (or alternatively subtracting the first equation from the second) gives. Note: let two circles with centres o and p touch each other at t. let ot = r1 and pt = r2 and r1 > r2. let the distance between their centres = op = d. it is clear from the figures that. • when the circles touch externally, d = r 1 r 2. • when the circles touch internally, d = r 1 r 2. 10th grade math.

Comments are closed.