Trigonometry Notes Graphing Sine And Cosine All Transformations 2020

Trigonometry Notes Graphing Sine And Cosine All Transformations 2020 Characteristics of sine and cosine functions. the sine and cosine functions have several distinct characteristics: they are periodic functions with a period of 2π. the domain of each function is (− ∞, ∞) and the range is [− 1, 1]. the graph of y = sin x is symmetric about the origin, because it is an odd function. Graphing sine and cosine trig functions ws #3 name date period ©y l2w0u1o8t mkquftka] [saojfbtswfaqrsen olplccx.k q uawlhll nrii`gghhtyse brgeas`edrzvaecdn. find the amplitude, the period in radians, the phase shift in radians, the vertical shift, and the minimum and maximum values. 1) y = 3cos.

College Trigonometry Unit 5 3 Notes Graphing Sine And Cosine With All 10: graphs of trigonometric functions. key terms. basic graphs. amplitude: one half of the vertical distance between the maxima and minima of a sine or cosine graph. asymptote: any line that a function approaches closely without ever intersecting. fundamental period: the smallest interval over which a periodic function repeats itself. Finding the 4 segments of trigonometric transformations: amplitude: increases the range from the midline, commonly multiplied in front of the function. example: = sin (0) y = 1 * 1, so y = 1. = 3 * sin (0) y = 3 * 1, so y = 3. midline: this is the vertical shift of the function. if no value is found for the midline, the default vertical shift is 0. As we saw in sine and cosine graphs, the graphs of the basic sine and cosine functions are as follows: sine function. cosine function. from these basic graphs, we can manipulate the functions to obtain new graphs by adding and multiplying by constants: \[\begin{align} y &= a \sin (b x c) d\\ y &= a \cos (b x c) d. \end{align}\]. Visualizing the amplitude of the sine function. when we look at the graph that is generated by unwrapping our unit circle, we will see that it generates a wave like graph, where the domain is all real numbers and the range is between 1 and 1. this is due to the fact that as we move around the unit circle in a counterclockwise fashion, we.

How To Graph Sine And Cosine Explained W 5 Terrific Examples As we saw in sine and cosine graphs, the graphs of the basic sine and cosine functions are as follows: sine function. cosine function. from these basic graphs, we can manipulate the functions to obtain new graphs by adding and multiplying by constants: \[\begin{align} y &= a \sin (b x c) d\\ y &= a \cos (b x c) d. \end{align}\]. Visualizing the amplitude of the sine function. when we look at the graph that is generated by unwrapping our unit circle, we will see that it generates a wave like graph, where the domain is all real numbers and the range is between 1 and 1. this is due to the fact that as we move around the unit circle in a counterclockwise fashion, we. Notes: the sine parent graph crosses through the origin. the sine and cosine parent graphs each oscillate between y = 1 and y = 1. the ordered pairs for these graphs were derived from the unit circle. to graph sine and cosine, use the general forms: [ ( )] [ ( )] transformations of the parent graphs can include: 1. Plot of the tangent function. the tangent function has a completely different shape it goes between negative and positive infinity, crossing through 0, and at every π radians (180°), as shown on this plot. at π 2 radians (90°), and at − π 2 (−90°), 3 π 2 (270°), etc, the function is officially undefined, because it could be.
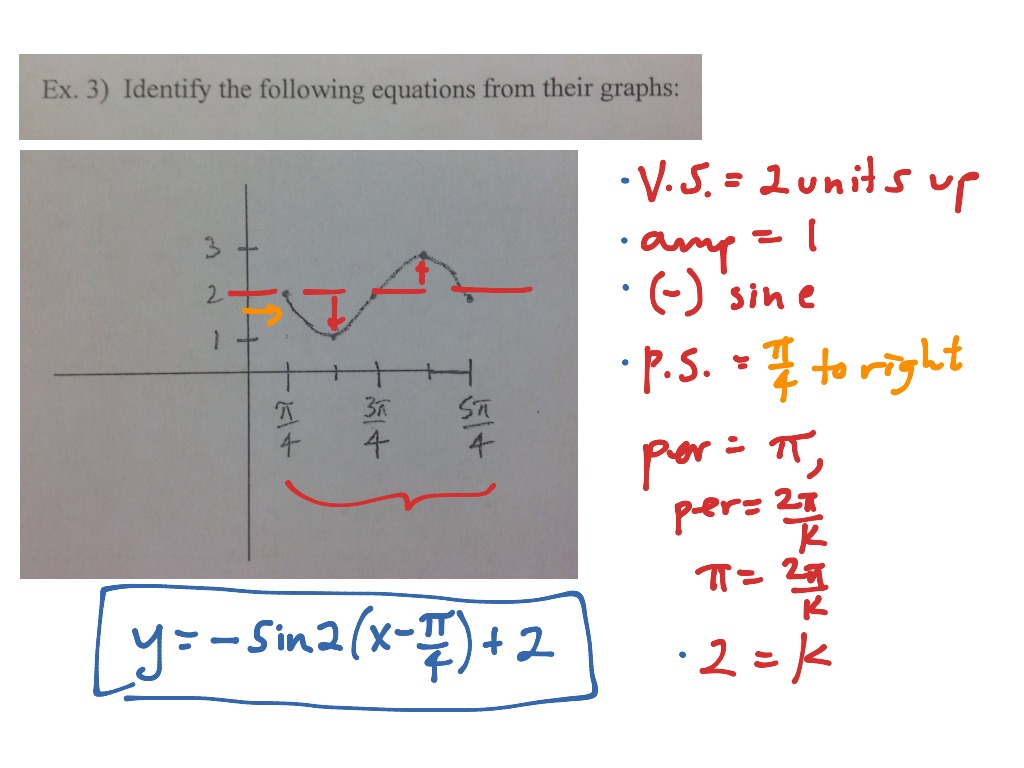
Graphing Sine And Cosine All Transformations Math Trigonometry Notes: the sine parent graph crosses through the origin. the sine and cosine parent graphs each oscillate between y = 1 and y = 1. the ordered pairs for these graphs were derived from the unit circle. to graph sine and cosine, use the general forms: [ ( )] [ ( )] transformations of the parent graphs can include: 1. Plot of the tangent function. the tangent function has a completely different shape it goes between negative and positive infinity, crossing through 0, and at every π radians (180°), as shown on this plot. at π 2 radians (90°), and at − π 2 (−90°), 3 π 2 (270°), etc, the function is officially undefined, because it could be.

Comments are closed.