Trigonometric Substitution
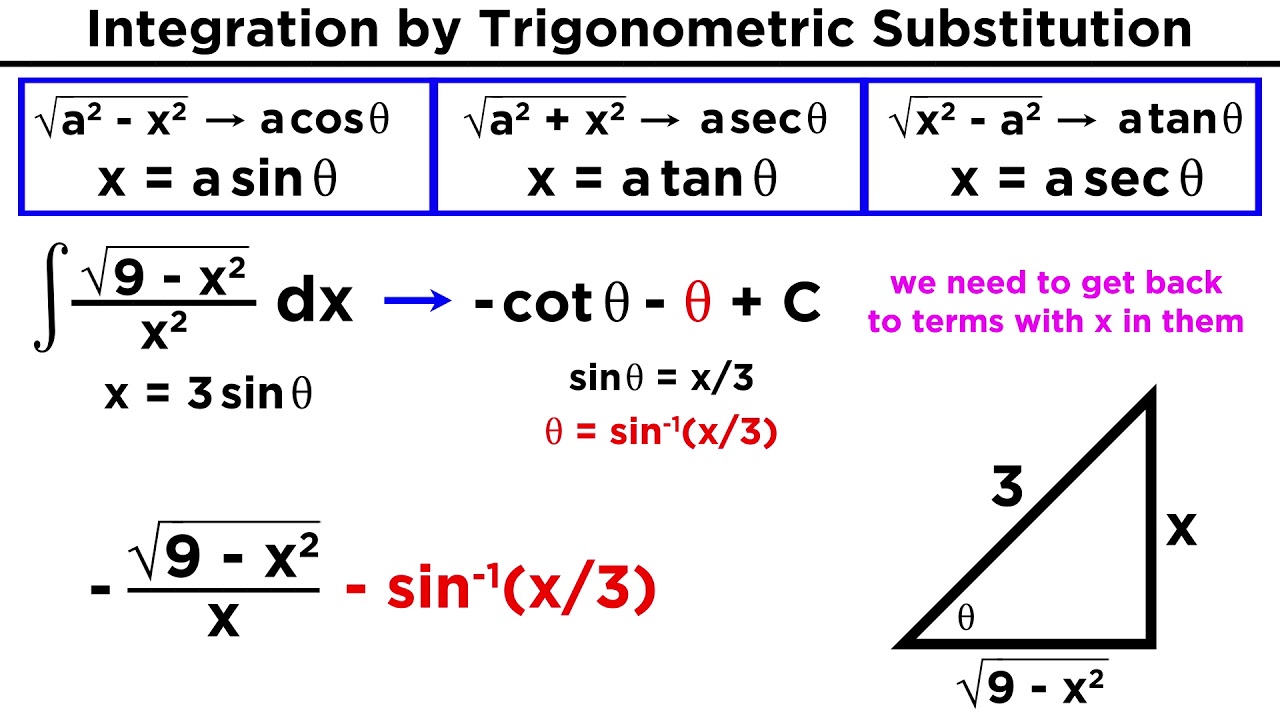
Integration By Trigonometric Substitution Youtube Learn how to use trigonometric substitution to evaluate integrals involving radicals of the form \\ (\\sqrt {a^2−x^2}\\), \\ (\\sqrt {a^2 x^2}\\), and \\ (\\sqrt {x^2−a^2}\\). see examples, formulas, and reference triangles for different substitutions. Learn how to use trig substitutions to integrate expressions with roots, such as √a2x2 − b2 or √a2 b2x2. see the general forms, the trig identities, and the definite integral cases for each substitution.
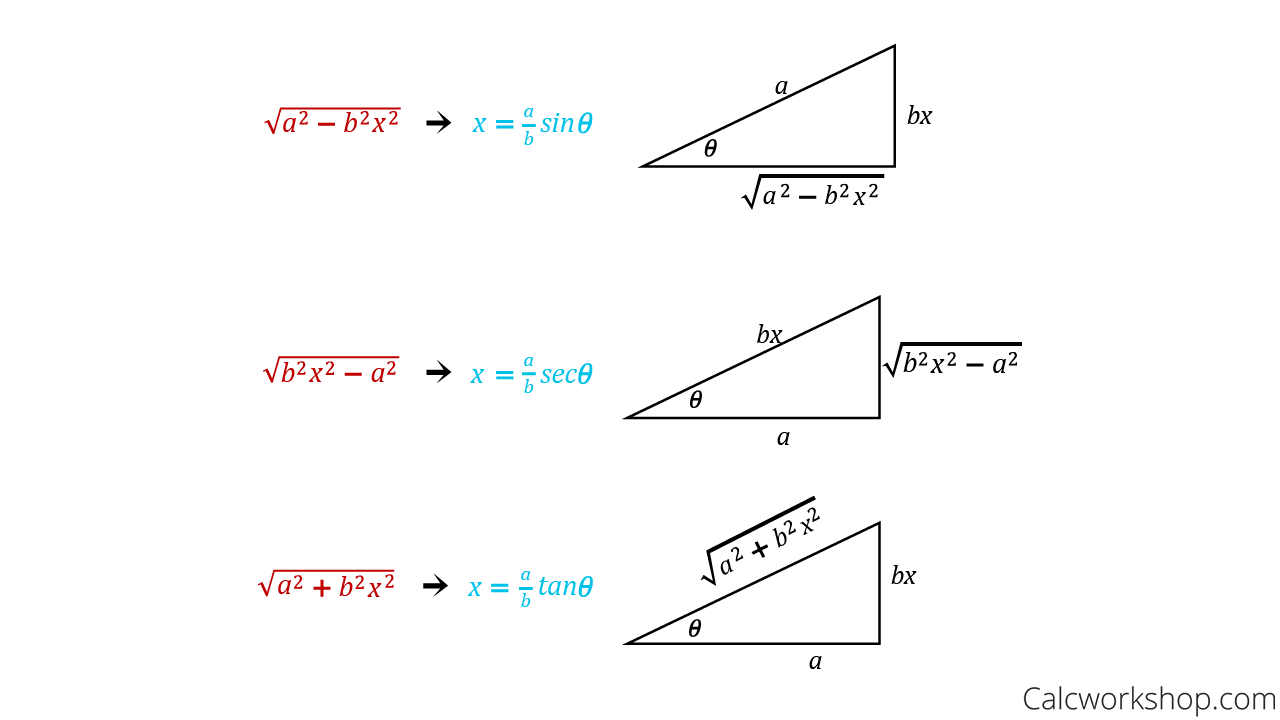
Trig Substitution Your New Best Friend In Calculus Learn how to use trigonometric substitutions to evaluate integrals involving radical functions. see examples, geometric constructions, and hyperbolic substitutions. We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. the technique of trigonometric substitution comes in very handy when evaluating these integrals. this technique uses substitution to rewrite these integrals as trigonometric integrals. integrals involving a 2 − x 2. Problems for section 7.6. integrals containing one of the terms. can often be integrated by a trigonometric substitution. the idea is to take x, a, and the square root as the three sides of a right triangle and use one of its acute angles as a new variable θ. the three kinds of trigonometric substitutions are shown in figure 7.6.1. Learn how to use trigonometric substitution to evaluate integrals with radicals involving trigonometric functions. see examples, sketches, and tips for choosing the right substitution.

Ppt 7 2 Trig Integrals Powerpoint Presentation Free Download Id Problems for section 7.6. integrals containing one of the terms. can often be integrated by a trigonometric substitution. the idea is to take x, a, and the square root as the three sides of a right triangle and use one of its acute angles as a new variable θ. the three kinds of trigonometric substitutions are shown in figure 7.6.1. Learn how to use trigonometric substitution to evaluate integrals with radicals involving trigonometric functions. see examples, sketches, and tips for choosing the right substitution. Lesson 16: trigonometric substitution. introduction to trigonometric substitution. substitution with x=sin (theta) more trig sub practice. trig and u substitution together (part 1) trig and u substitution together (part 2) trig substitution with tangent. more trig substitution with tangent. long trig sub problem. Learn how to use trigonometric substitution to evaluate integrals of the form \\int \\sqrt {a^2 x^2} dx. see examples, definitions, and generalizations of this method.

Trigonometry Formulas And Identities Full List Teachoo Lesson 16: trigonometric substitution. introduction to trigonometric substitution. substitution with x=sin (theta) more trig sub practice. trig and u substitution together (part 1) trig and u substitution together (part 2) trig substitution with tangent. more trig substitution with tangent. long trig sub problem. Learn how to use trigonometric substitution to evaluate integrals of the form \\int \\sqrt {a^2 x^2} dx. see examples, definitions, and generalizations of this method.

Comments are closed.