Trigonometric Identities A Plus Topper

Trigonometric Identities A Plus Topper Trigonometric identities (1) conditional trigonometrical identities we have certain trigonometric identities. like sin2 θ cos2 θ = 1 and 1 tan2 θ = sec2 θ etc. such identities are identities in the sense that they hold for all value of the angles which satisfy the given condition among them and they are called […]. Trigonometric identities. in algebraic form, an identity in x is satisfied by some particular value of x. for example (x 1) 2 =x 2 2x 1 is an identity in x. it is satisfied for all values of x. the same applies to trigonometric identities also. the equations can be seen as facts written in a mathematical form, that is true for “right angle.

Trigonometric Identities A Plus Topper Trigonometrical ratios or functions. in the right angled triangle omp, we have base = om = x, perpendicular =pm = y and hypotenues = op =r. we define the following trigonometric ratio which are also known as trigonometric function. (1) relation between trigonometric ratios (functions) sin θ . cosec θ = 1. tan θ . cot θ = 1. Here we have given ml aggarwal class 10 solutions for icse maths chapter 19 trigonometric identities chapter test. ml aggarwal solutions icse solutions selina icse solutions. question 1. (i) if θ is an acute angle and cosec θ = √5 find the value of cot θ – cos θ. (ii) if θ is an acute angle and tan θ = 8 15 8 15, find the value of sec. For the next trigonometric identities we start with pythagoras' theorem: the pythagorean theorem says that, in a right triangle, the square of a plus the square of b is equal to the square of c: a 2 b 2 = c 2. dividing through by c2 gives. a2 c2 b2 c2 = c2 c2. this can be simplified to: (a c)2 (b c)2 = 1. 1 tan2θ = 1 (sinθ cosθ)2 rewrite left side = (cosθ cosθ)2 (sinθ cosθ)2 write both terms with the common denominator = cos2θ sin2θ cos2θ = 1 cos2θ = sec2θ. recall that we determined which trigonometric functions are odd and which are even. the next set of fundamental identities is the set of even odd identities.

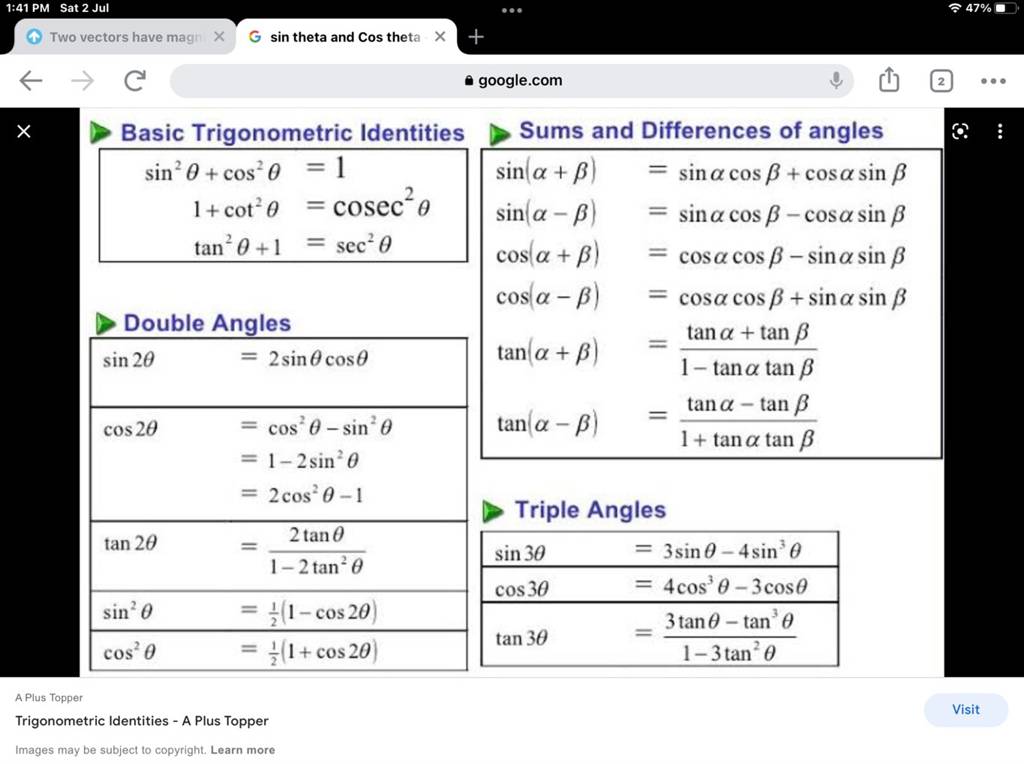
A Plus Topper Trigonometric Identities A Plus Topper Visit Images May B For the next trigonometric identities we start with pythagoras' theorem: the pythagorean theorem says that, in a right triangle, the square of a plus the square of b is equal to the square of c: a 2 b 2 = c 2. dividing through by c2 gives. a2 c2 b2 c2 = c2 c2. this can be simplified to: (a c)2 (b c)2 = 1. 1 tan2θ = 1 (sinθ cosθ)2 rewrite left side = (cosθ cosθ)2 (sinθ cosθ)2 write both terms with the common denominator = cos2θ sin2θ cos2θ = 1 cos2θ = sec2θ. recall that we determined which trigonometric functions are odd and which are even. the next set of fundamental identities is the set of even odd identities. To verify that equation (1) is an identity, we work with the expression tan2(x) 1. it can often be a good idea to write all of the trigonometric functions in terms of the cosine and sine to start. in this case, we know that tan(t) = sin(t) cos(t), so we could begin by making this substitution to obtain the identity. Trigonometric identities are the equalities that involve trigonometry functions and holds true for all the values of variables given in the equation. there are various distinct trigonometric identities involving the side length as well as the angle of a triangle. the trigonometric identities hold true only for the right angle triangle.

Solution Trigonometric Identities A Plus Topper Studypool To verify that equation (1) is an identity, we work with the expression tan2(x) 1. it can often be a good idea to write all of the trigonometric functions in terms of the cosine and sine to start. in this case, we know that tan(t) = sin(t) cos(t), so we could begin by making this substitution to obtain the identity. Trigonometric identities are the equalities that involve trigonometry functions and holds true for all the values of variables given in the equation. there are various distinct trigonometric identities involving the side length as well as the angle of a triangle. the trigonometric identities hold true only for the right angle triangle.

Trigonometric Identities A Plus Topper

Using All Trigonometric Identities A Plus Topper