Trig Values Of Special Angles Part 1

Trig Values Of Special Angles Youtube How to evaluate trig functions of special angles? easy way to use right triangle and label sides to find sin, cos, tan, cot, csc, and sec of the special angles, and of angles at multiples of 90°. this is part 1. scroll down the page for part 2. example: find cos 90, tan 90, sin 630, sin 135, tan ( 405), sin 210, tan ( 30). show video lesson. This lesson shows how to find the trig ratios of the special angles and how to use them to find exact values of expressions involving sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees. this is conclusion of a two part lesson. the trigonometric function values of 30, 45, and 60 degrees and their corresponding radian measure.
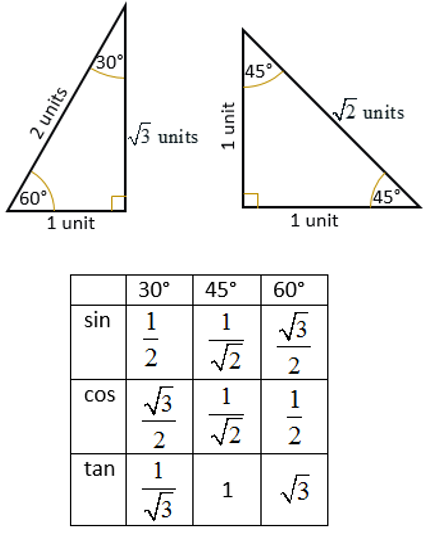
Trigonometric Ratios Of Special Angles 0 30 45 60 90 Solutions This lesson shows how to find the trig ratios of the special angles and how to use them to find exact values of expressions involving sine, cosine and tangen. With your palm facing you, count off the basic reference angles, starting with your thumb: 0°, 30°, 45°, 60°, and 90°. to find a trig value, you'll lower the finger corresponding to that angle, keeping your palm facing you. for the sine value, you'll take the square root of the number of fingers to the left of the lowered finger, and. How to find the trig ratios of the special angles? this video shows how to find the trig ratios of the special angles and how to use them to find exact values of expressions involving sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees. this is the first part of a two part lesson. scroll down for part 2. show video lesson. Since the value of sin30° (= 1 2) sin 30° (= 1 2), is an exact value that can also be easily remembered, we say that 30º is a special trigonometric angle. other special trigonometric angles where the trigonometric ratios give simple, exact values include 0° (or 360º), 45°, 60°, 90°, 180º and 270º.

Trig Ratios Of Special Angles Part 1 Youtube How to find the trig ratios of the special angles? this video shows how to find the trig ratios of the special angles and how to use them to find exact values of expressions involving sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees. this is the first part of a two part lesson. scroll down for part 2. show video lesson. Since the value of sin30° (= 1 2) sin 30° (= 1 2), is an exact value that can also be easily remembered, we say that 30º is a special trigonometric angle. other special trigonometric angles where the trigonometric ratios give simple, exact values include 0° (or 360º), 45°, 60°, 90°, 180º and 270º. Case 1: special angle 45o (from a 45o – 45o – 90o triangle) the following figure 7 1 represents a 45 ∘ – 45 ∘ – 90 ∘ isosceles right triangle with two 45 ∘ degree angles. the lengths of the three legs of the right triangle are named a, b, and c. the angles opposite the legs of lengths a, b, and c are named a, b, and c. If the reference angle is a special angle (0, 30, 45, 60, 90 degrees), then you can find exact trig values without a calculator. for example, find cos(81 pi 4). use the rrqss method. free, unlimited, online practice.

Special Angles In Trigonometry Functions Values Video Lesson Case 1: special angle 45o (from a 45o – 45o – 90o triangle) the following figure 7 1 represents a 45 ∘ – 45 ∘ – 90 ∘ isosceles right triangle with two 45 ∘ degree angles. the lengths of the three legs of the right triangle are named a, b, and c. the angles opposite the legs of lengths a, b, and c are named a, b, and c. If the reference angle is a special angle (0, 30, 45, 60, 90 degrees), then you can find exact trig values without a calculator. for example, find cos(81 pi 4). use the rrqss method. free, unlimited, online practice.

Comments are closed.