Trig Substitution Your New Best Friend In Calculus

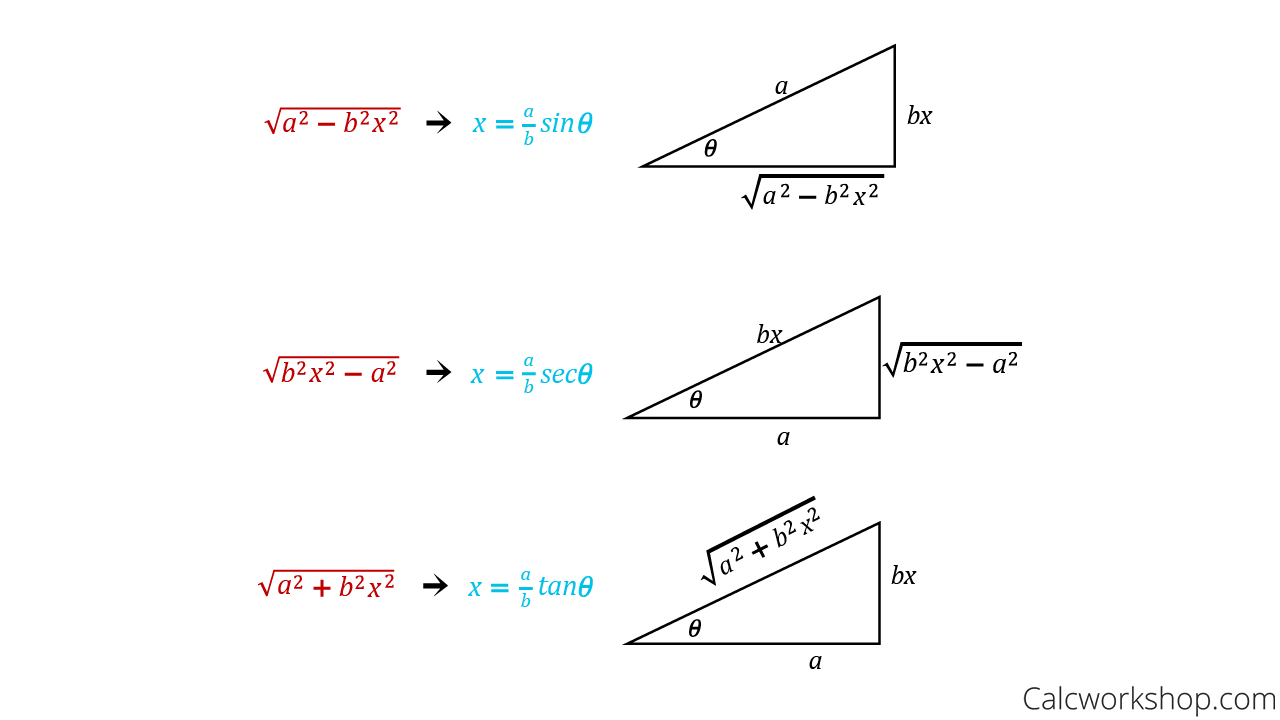
Trig Substitution Your New Best Friend In Calculus Your new best friend in calculus. here’s a helpful tip. when things are complicated, us a substitution rule to make things easier! in particular, trigonometric substitution, also called inverse substitution, is a way for us to take a difficult radical expression and transform it into a manageable trigonometric expression. the idea is to use. Section 7.3 : trig substitutions. as we have done in the last couple of sections, let’s start off with a couple of integrals that we should already be able to do with a standard substitution. ∫x√25x2 − 4dx = 1 75(25x2 − 4)3 2 c ∫ x √25x2 − 4 dx = 1 25√25x2 − 4 c. both of these used the substitution u = 25x2 − 4 and at.

Trigonometric Substitution 6 Integral Calculus Youtube The substitution , then the identity allows us to get rid of the root sign because notice the difference between the substitution (in which the new variable is a function of the old one) and the substitution (the old variable is a function of the new one). in general we can make a substitution of the form by using the substitution rule in reverse. That looks like this, we will use a strategy called trig substitution, in which we use u substitution combined with the pythagorean identities sin2(x) cos2(x) = 1 and tan2(x) 1 = sec2(x) instead of using a ufor our substitution, we will use θ. we show this substitution process for the three types of square roots highlighted above: √ a2. Lecture 4: trigonometric substitution calculus ii, section 3 january 31, 2022 so far, the primary methods of integration we know are u substitution and integration by parts. today, we’re going to use those to create more methods: first, we’ll use integration by parts (among other tools) to compute some trigonometric integrals, and once we know. With practice, you will gain insight into what kind of substitution will work best for a particular integral. key concepts trigonometric substitutions are often useful for integrals containing factors of the form \[(a^2 x^2)^n,\qquad\qquad (x^2 a^2)^n,\qquad {\small\textrm{or}}\qquad (x^2 a^2)^n.\].

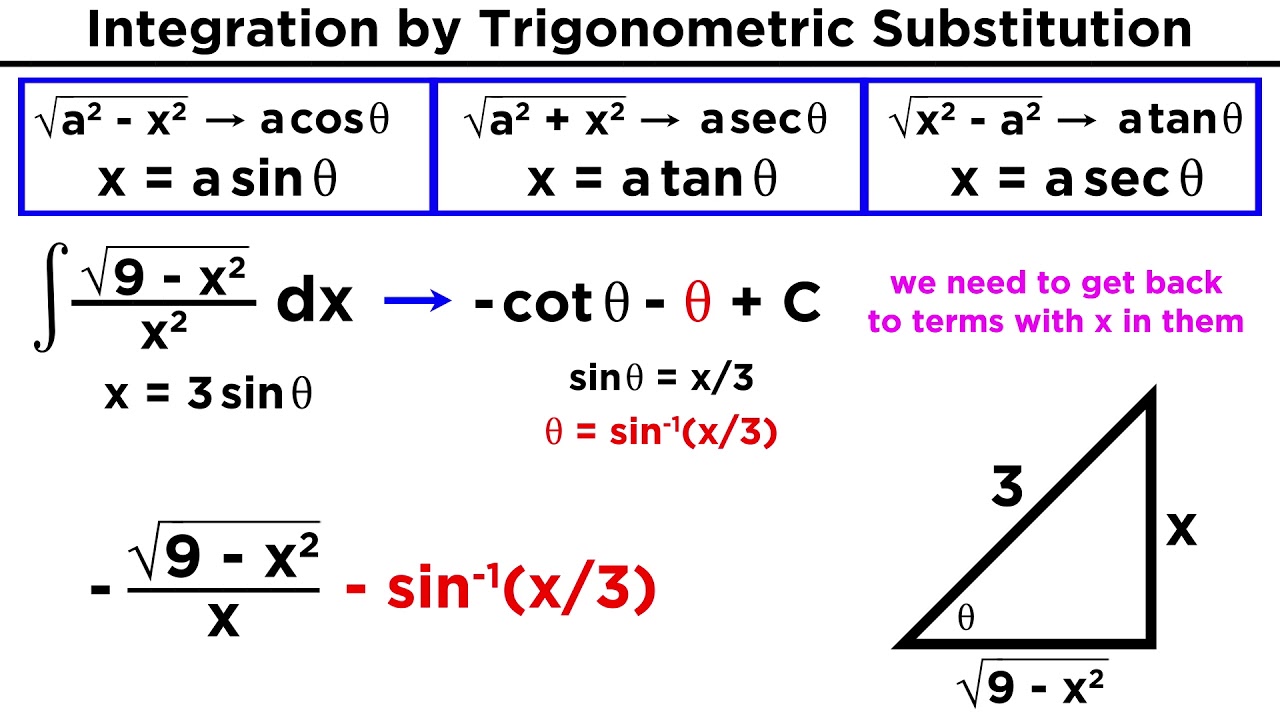
Integration By Trigonometric Substitution Youtube Lecture 4: trigonometric substitution calculus ii, section 3 january 31, 2022 so far, the primary methods of integration we know are u substitution and integration by parts. today, we’re going to use those to create more methods: first, we’ll use integration by parts (among other tools) to compute some trigonometric integrals, and once we know. With practice, you will gain insight into what kind of substitution will work best for a particular integral. key concepts trigonometric substitutions are often useful for integrals containing factors of the form \[(a^2 x^2)^n,\qquad\qquad (x^2 a^2)^n,\qquad {\small\textrm{or}}\qquad (x^2 a^2)^n.\]. Back to problem list. 11. use a trig substitution to evaluate ∫ t3(3t2 −4)5 2 dt ∫ t 3 (3 t 2 − 4) 5 2 d t. first, do not get excited about the exponent in the integrand. these types of problems work exactly the same as those with just a root (as opposed to this case in which we have a root to a power – you do agree that is what we. This session also covers the trigonometry needed to convert your answer to a more useful form. lecture video and notes video excerpts. clip 1: example of trig substitution. clip 2: undoing trig substitution. clip 3: summary of trig substitution. worked example. substitution practice. problem (pdf) solution (pdf) recitation video hyperbolic trig.

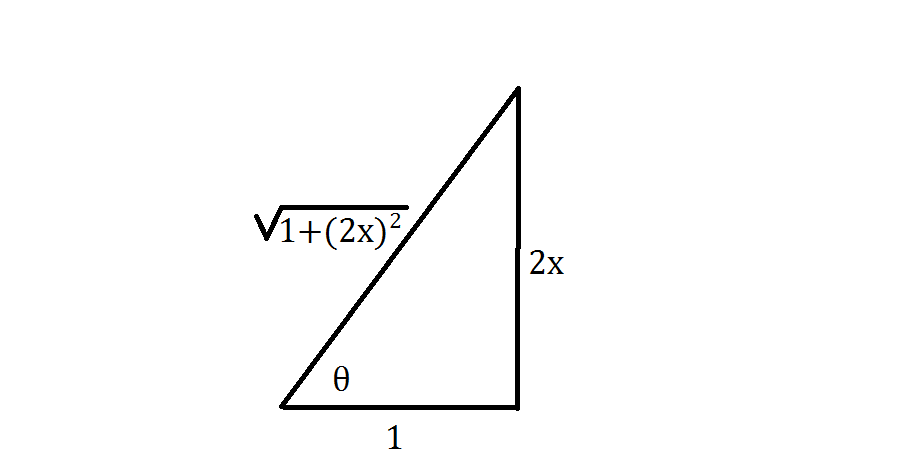
Trig Substitution Your New Best Friend In Calculus 77d Back to problem list. 11. use a trig substitution to evaluate ∫ t3(3t2 −4)5 2 dt ∫ t 3 (3 t 2 − 4) 5 2 d t. first, do not get excited about the exponent in the integrand. these types of problems work exactly the same as those with just a root (as opposed to this case in which we have a root to a power – you do agree that is what we. This session also covers the trigonometry needed to convert your answer to a more useful form. lecture video and notes video excerpts. clip 1: example of trig substitution. clip 2: undoing trig substitution. clip 3: summary of trig substitution. worked example. substitution practice. problem (pdf) solution (pdf) recitation video hyperbolic trig.

Trigonometric Substitution Examples Solutions Videos

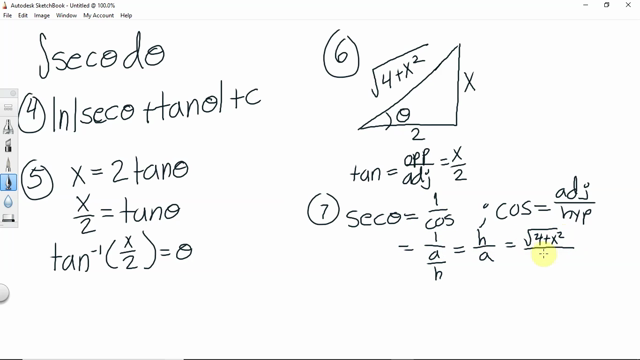
Trig Substitution Calculus 2 Bc Numerade