Trig Substitution Integrals Cheat Sheet Example With Solution Youtube

Trig Substitution Integrals Cheat Sheet Example With Solution Youtube Is trig sub hard? not if you watch this video! this trig substitution cheat sheet leads you through the logic behind how trig sub works and gives you the sho. My integrals course: kristakingmath integrals coursethis video is all about how to start a trigonometric substitution problem so that you'l.

Trigonometric Substitution 6 Integral Calculus Youtube Mit grad shows how to integrate using trigonometric substitution. to skip ahead: 1) for how to know which trig substitution to use (sin, tan, or sec), skip t. Example 4 find . solution it would be possible to use the trigonometric substitution here (as in example 3). but the direct substitution is simpler, because then and note example 4 illustrates the fact that even when trigonometric substitutions are pos sible, they may not give the easiest solution. you should look for a simpler method first. Here is a summary for the sine trig substitution. √a2 − b2x2 ⇒ x = a bsinθ, − π 2 ≤ θ ≤ π 2. there is one final case that we need to look at. the next integral will also contain something that we need to make sure we can deal with. example 5 evaluate the following integral. ∫ 1 60 x5 (36x2 1)3 2 dx. show solution. Examples of such expressions are $$ \displaystyle{ \sqrt{ 4 x^2 }} \ \ \ and \ \ \ \displaystyle{(x^2 1)^{3 2}} $$ the method of trig substitution may be called upon when other more common and easier to use methods of integration have failed. trig substitution assumes that you are familiar with standard trigonometric identies, the use of.

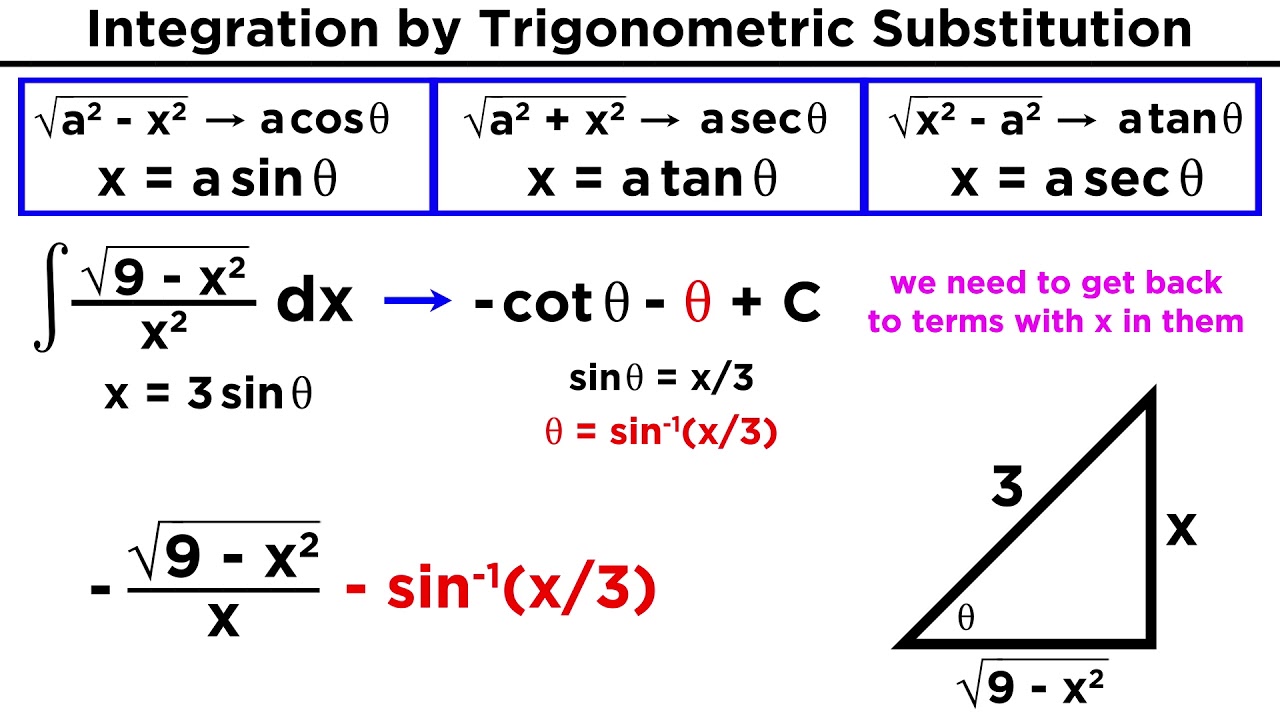
Integration By Trigonometric Substitution Youtube Here is a summary for the sine trig substitution. √a2 − b2x2 ⇒ x = a bsinθ, − π 2 ≤ θ ≤ π 2. there is one final case that we need to look at. the next integral will also contain something that we need to make sure we can deal with. example 5 evaluate the following integral. ∫ 1 60 x5 (36x2 1)3 2 dx. show solution. Examples of such expressions are $$ \displaystyle{ \sqrt{ 4 x^2 }} \ \ \ and \ \ \ \displaystyle{(x^2 1)^{3 2}} $$ the method of trig substitution may be called upon when other more common and easier to use methods of integration have failed. trig substitution assumes that you are familiar with standard trigonometric identies, the use of. A cheat sheet for integrals with step by step solutions to mathematical problems. The trigonometric identity we shall use here is one of the ‘double angle’ formulae: cos 2a = 1 − 2 sin2 a. by rearranging this we can write. sin2 a =. (1 − cos 2a) notice that by using this identity we can convert an expression involving sin2 has no powers in. therefore, our integral can be written. into one which.