Trig Ratios Of Special Angles Part 1

Trig Ratios Of Special Angles Part 1 Youtube This lesson shows how to find the trig ratios of the special angles and how to use them to find exact values of expressions involving sine, cosine and tangen. How to evaluate trig functions of special angles? easy way to use right triangle and label sides to find sin, cos, tan, cot, csc, and sec of the special angles, and of angles at multiples of 90°. this is part 1. scroll down the page for part 2. example: find cos 90, tan 90, sin 630, sin 135, tan ( 405), sin 210, tan ( 30). show video lesson.
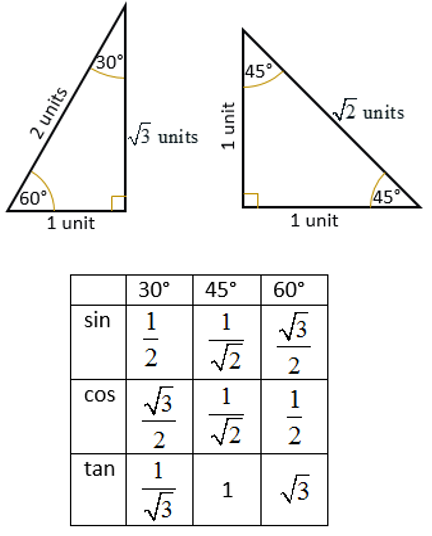
Trigonometric Ratios Of Special Angles 0 30 45 60 90 Solutions This lesson shows how to find the trig ratios of the special angles and how to use them to find exact values of expressions involving sine, cosine and tangent values of 0, 30, 45, 60 and 90 degrees. this is conclusion of a two part lesson. the trigonometric function values of 30, 45, and 60 degrees and their corresponding radian measure. Since the value of sin30° (= 1 2) sin 30° (= 1 2), is an exact value that can also be easily remembered, we say that 30º is a special trigonometric angle. other special trigonometric angles where the trigonometric ratios give simple, exact values include 0° (or 360º), 45°, 60°, 90°, 180º and 270º. These two angles form a 30˚ 60˚ 90˚ right triangle as shown. the ratio of the sides of the triangle is 1:√3:2. from the triangle we get the ratios as follows: special angles: 45 and 90. next, we consider the 45˚ angle that forms a 45˚ 45˚ 90˚ right triangle as shown. the ratio of the sides of the triangle is. combining the two tables. With your palm facing you, count off the basic reference angles, starting with your thumb: 0°, 30°, 45°, 60°, and 90°. to find a trig value, you'll lower the finger corresponding to that angle, keeping your palm facing you. for the sine value, you'll take the square root of the number of fingers to the left of the lowered finger, and.

Trig Values Of Special Angles Youtube These two angles form a 30˚ 60˚ 90˚ right triangle as shown. the ratio of the sides of the triangle is 1:√3:2. from the triangle we get the ratios as follows: special angles: 45 and 90. next, we consider the 45˚ angle that forms a 45˚ 45˚ 90˚ right triangle as shown. the ratio of the sides of the triangle is. combining the two tables. With your palm facing you, count off the basic reference angles, starting with your thumb: 0°, 30°, 45°, 60°, and 90°. to find a trig value, you'll lower the finger corresponding to that angle, keeping your palm facing you. for the sine value, you'll take the square root of the number of fingers to the left of the lowered finger, and. Pythagorean’s theorem. 2 2 = 2. example 1: in right triangle. with the right angle find. if. = 4√5 and = 4. two special triangles are 30° − 60° − 90° triangles and 45° − 45° − 90° triangles. in such triangles, sides are proportional. you need to know the length of one side only to find the remaining sides. Trigonometric ratios of some specific angle are defined as the ratio of the sides of a right angle triangle with respect to any of its acute angles. trigonometric ratios of some specific angles include 0°, 30°, 45°, 60° and 90°. now, let us learn how to find the trigonometric ratios of these angles in detail.

Special Angle Trig Ratios Chart Free Download Pythagorean’s theorem. 2 2 = 2. example 1: in right triangle. with the right angle find. if. = 4√5 and = 4. two special triangles are 30° − 60° − 90° triangles and 45° − 45° − 90° triangles. in such triangles, sides are proportional. you need to know the length of one side only to find the remaining sides. Trigonometric ratios of some specific angle are defined as the ratio of the sides of a right angle triangle with respect to any of its acute angles. trigonometric ratios of some specific angles include 0°, 30°, 45°, 60° and 90°. now, let us learn how to find the trigonometric ratios of these angles in detail.

Special Triangles Trig Ratios 2 1c Pre Calculus 11 Youtube
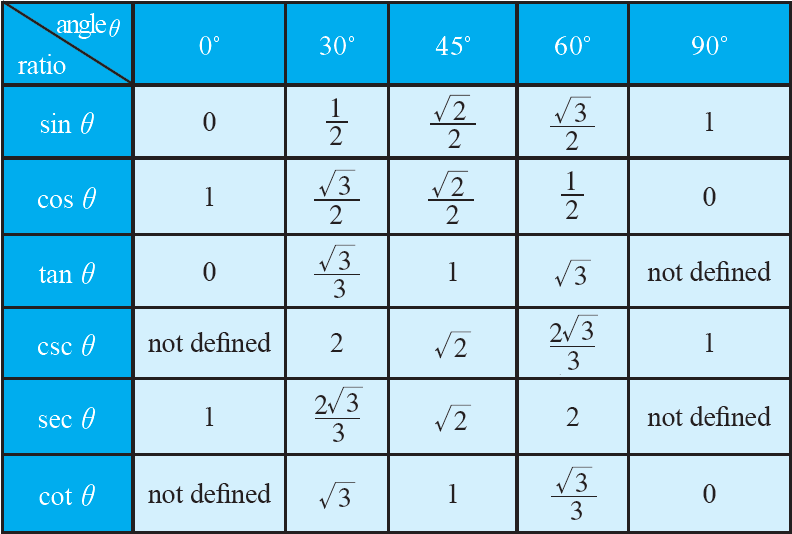
Trigonometric Ratios Of Special Angles

Comments are closed.