Trig 1 1 Angles

Trigonometric Ratios And Special Angles Youtube An angle is a right angle if it equals 90° 90 °. . an angle is obtuse if it is between 90° 90 °. and 180° 180 °. . an angle is a straight angle if it equals 180° 180 °. . figure 1.1.1 types of angles. in elementary geometry, angles are always considered to be positive and not larger than 360 ∘. Figure 1.4.2 angle greater than 360 . we can now define the trigonometric functions of any angle in terms of cartesian coordinates. recall that the xy coordinate plane consists of points denoted by pairs (x, y) of real numbers. the first number, x, is the point's x coordinate, and the second number, y, is its y coordinate.

Trig Values Of Special Angles Youtube To get to this answer: take the sin of any of the 45° angles, which equals any of the legs (a) divided by the hypotenuse (c): sin (45°) = a c. solve for the leg (a): a = c × sin (45°) remember that sin (45°) = 1 √2 and input the hypotenuse c = 18 cm: a = 18 cm × (1 √2):. 1 tan²θ = sec²θ. 1 cot²θ = csc²θ. reciprocal identities: these identities define the relationships between each trigonometric function and its reciprocal. cscθ = 1 sinθ. secθ = 1 cosθ. cotθ = 1 tanθ. quotient identities: these identities show that tangent and cotangent are ratios of sine and cosine. The trigonometric function (also called the 'trig function') of f(x) = sinθ has a domain, which is the angle θ given in degrees or radians, and a range of [ 1, 1]. similarly we have the domain and range from all other functions. Tan, cot, sec, and csc, calculated from trig identities. once you know the value of sine and cosine, you can use the following trigonometric identities to obtain the values of the other four functions: tangent is the sine to cosine ratio. tan(α) = sin(α) cos(α) cosecant is the reciprocal of the sine. csc(α) = 1 sin(α).
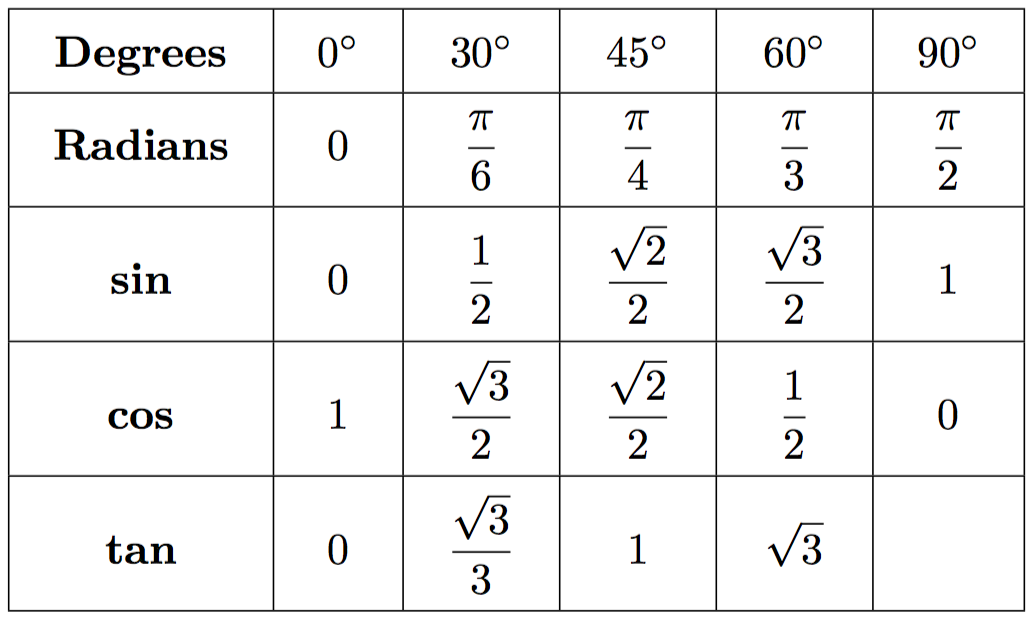
Basic Trigonometric Identities The trigonometric function (also called the 'trig function') of f(x) = sinθ has a domain, which is the angle θ given in degrees or radians, and a range of [ 1, 1]. similarly we have the domain and range from all other functions. Tan, cot, sec, and csc, calculated from trig identities. once you know the value of sine and cosine, you can use the following trigonometric identities to obtain the values of the other four functions: tangent is the sine to cosine ratio. tan(α) = sin(α) cos(α) cosecant is the reciprocal of the sine. csc(α) = 1 sin(α). Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more! right angled triangle. the triangle of most interest is the right angled triangle. the right angle is shown by the little box in the corner: another angle is often labeled θ, and the three sides are then called:. Example of right triangle trigonometry calculations with steps. take a right triangle with hypotenuse c = 5 c = 5 and an angle \alpha=38\degree α= 38°. surprisingly enough, this is enough data to fully solve the right triangle! follow these steps: calculate the third angle: β = 90 ° − α. \beta = 90\degree \alpha β = 90°−α.

Trig 1 1 Angles Youtube Trigonometry helps us find angles and distances, and is used a lot in science, engineering, video games, and more! right angled triangle. the triangle of most interest is the right angled triangle. the right angle is shown by the little box in the corner: another angle is often labeled θ, and the three sides are then called:. Example of right triangle trigonometry calculations with steps. take a right triangle with hypotenuse c = 5 c = 5 and an angle \alpha=38\degree α= 38°. surprisingly enough, this is enough data to fully solve the right triangle! follow these steps: calculate the third angle: β = 90 ° − α. \beta = 90\degree \alpha β = 90°−α.

Reference Angle Calculator Trig At Dianne Corriveau Blog

Comments are closed.