Triangle Sides And Angles Geogebra
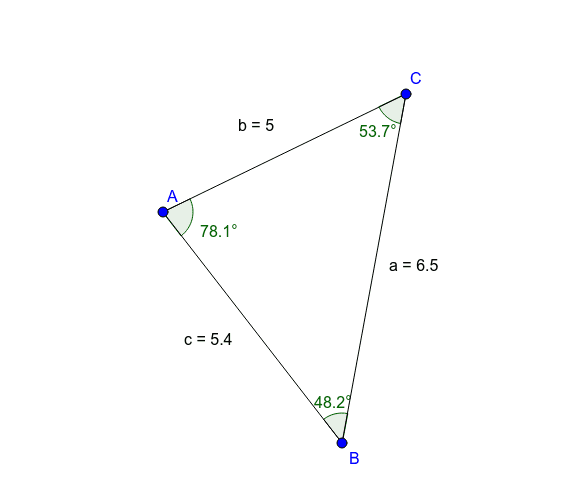
Triangle Sides And Angles Geogebra Adjust the angles in the triangle by dragging the endpoints along the circles. triangles by side lengths 1. create a scalene triangle. a scalene triangle has no congruent sides. 2. create an isosceles triangle. an isosceles triangle has 2 congruent sides. 3. create an equilateral triangle. Topic: angles. move the points a, b and c to create your own triangle. which side length is the longest? which angle is the largest? which side length is the smallest? which angle is the smallest? create another triangle and investigate the same questions? can you generalise a relationship between side lengths of a triangle and angles of triangle.
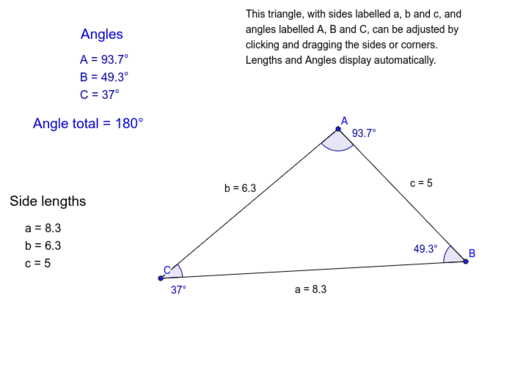
Basic Triangle With Adjustable Side Lengths And Angles Geogebra In this activity you will create triangles with right, obtuse, and acute angles and isosceles, scalene, and equilateral triangles. you will define each triangles side and angle then change each triangle to a different angle and side. this activity will meet standard ccss.math.content.4.g.a.1. when you define a triangle state its angle and sides. How to draw triangle in geogebra & find the sides length & interior anglesvideo made by: john albert buenaventuraweb app: geogebra.org geometry#. Now, let's check how finding the angles of a right triangle works: refresh the calculator. pick the option you need. assume that we have two sides, and we want to find all angles. the default option is the right one. enter the side lengths. our right triangle has a hypotenuse equal to 13 in and a leg a = 5 in. missing side and angles appear. in. To construct a triangle when the length of a side, hypotenuse, the angle at which right angle is formed are given, four steps are involved. step 1: draw a rough sketch of the triangle with given measure. step 2: first to draw the side whose length is given use the tool "line" in the tool bar and select the option "segment with given length".
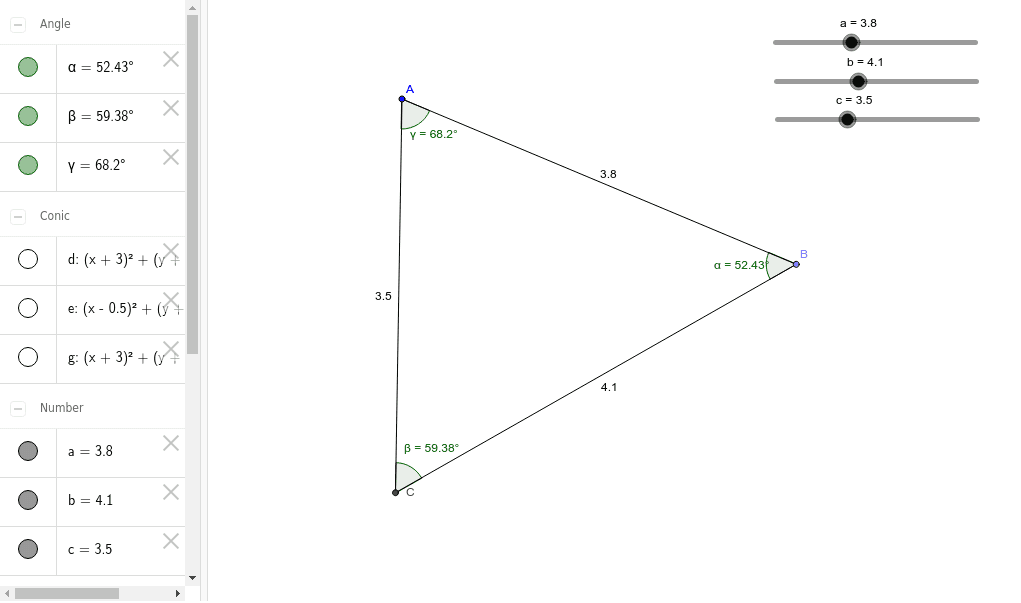
Triangle Sides And Angles Geogebra Now, let's check how finding the angles of a right triangle works: refresh the calculator. pick the option you need. assume that we have two sides, and we want to find all angles. the default option is the right one. enter the side lengths. our right triangle has a hypotenuse equal to 13 in and a leg a = 5 in. missing side and angles appear. in. To construct a triangle when the length of a side, hypotenuse, the angle at which right angle is formed are given, four steps are involved. step 1: draw a rough sketch of the triangle with given measure. step 2: first to draw the side whose length is given use the tool "line" in the tool bar and select the option "segment with given length". The 45° 45° 90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45° 45° 90°, follow a ratio of 1:1:√ 2. like the 30° 60° 90° triangle, knowing one side length allows you to determine the lengths of the other sides. Law of sines: the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. using the law of sines makes it possible to find unknown angles and sides of a triangle given enough information. where sides a, b, c, and angles a, b, c are as depicted in the above calculator, the law of sines can be written as shown.

Ordering Triangle Angles By Side Lengths Geogebra The 45° 45° 90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45° 45° 90°, follow a ratio of 1:1:√ 2. like the 30° 60° 90° triangle, knowing one side length allows you to determine the lengths of the other sides. Law of sines: the ratio of the length of a side of a triangle to the sine of its opposite angle is constant. using the law of sines makes it possible to find unknown angles and sides of a triangle given enough information. where sides a, b, c, and angles a, b, c are as depicted in the above calculator, the law of sines can be written as shown.

Comments are closed.