Triangle Side Angle Relationships

Triangle Side Angle Relationships Youtube Rule 1: interior angles sum up to 1800 180 0. rule 2: sides of triangle triangle inequality theorem : this theorem states that the sum of the lengths of any 2 sides of a triangle must be greater than the third side. rule 3: relationship between measurement of the sides and angles in a triangle: the largest interior angle and side are. Relationship of sides to interior angles in a triangle. in any triangle: the shortest side is always opposite the smallest interior angle. the longest side is always opposite the largest interior angle. try this drag the orange dots on the triangle below. options.
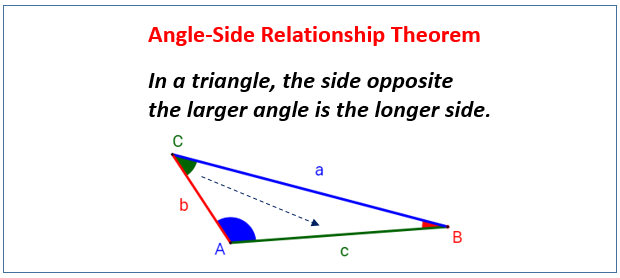
Triangle Inequality Angle Side Relationship Video Lessons Examples Concepts. 1 the longest side in a triangle is opposite the largest angle, and the shortest side is opposite the smallest angle. 2 triangle inequality: in any triangle, the sum of the lengths of any two sides is greater than the length of the third side. 3 pythagorean theorem: in a right triangle with hypotenuse c c, a2 b2 = c2 a 2 b 2 = c 2. Relation between sides and angles in a triangle. theorem. in a triangle, the longest side is opposite the largest angle. in other words, the largest angle lies opposite the longest side, the mid sized angle lies opposite the mid sized side, the smallest angle lies opposite the shortest side. theorem on the relation between sides and angles. 1. since in triangles the greatest angles face the longest sides, the measure of the angle x must be more than 44° given that it faces the 18 units side while the 44° angle faces a 15 units side. therefore, the only possible option from the choices is 55°. 2. since in triangles the greatest angles face the longest sides, the measure of the. Answer: the length of the third side of the triangle is 7.63 units. example 3: in triangle abc, ∠c = 42° and ∠a = 33°, and the side opposite to angle c is 12.5 units. find the length of the side of the triangle opposite to angle a. solution: we have ∠c = 42° and ∠a = 33°, c = 12.5 units. we need to find the side 'a'.
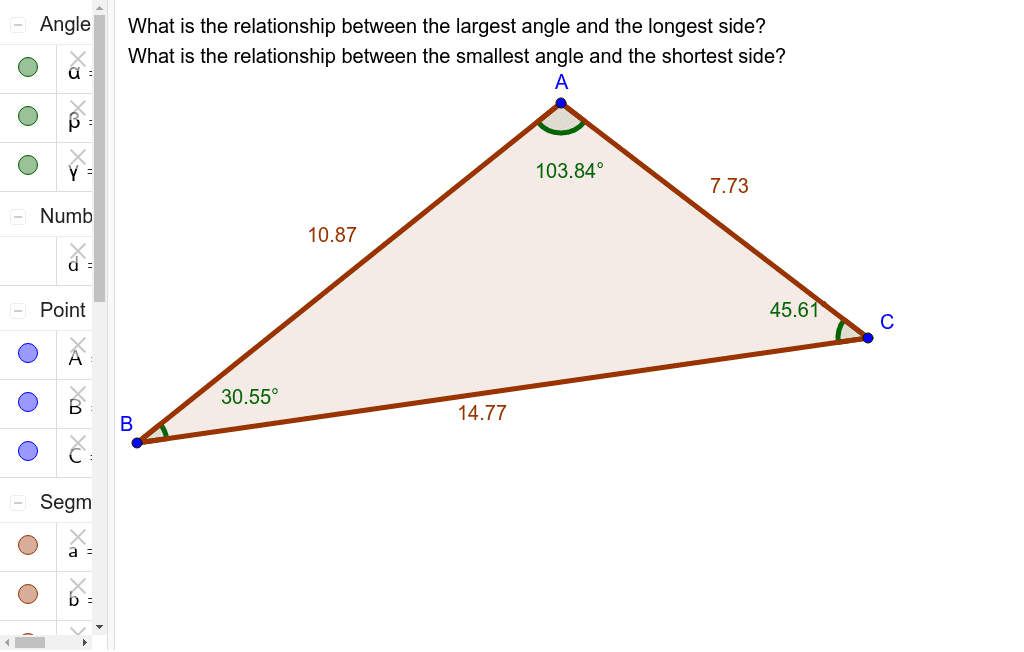
Side Angle Relationships In A Triangle Geogebra 1. since in triangles the greatest angles face the longest sides, the measure of the angle x must be more than 44° given that it faces the 18 units side while the 44° angle faces a 15 units side. therefore, the only possible option from the choices is 55°. 2. since in triangles the greatest angles face the longest sides, the measure of the. Answer: the length of the third side of the triangle is 7.63 units. example 3: in triangle abc, ∠c = 42° and ∠a = 33°, and the side opposite to angle c is 12.5 units. find the length of the side of the triangle opposite to angle a. solution: we have ∠c = 42° and ∠a = 33°, c = 12.5 units. we need to find the side 'a'. Angle side relationships in a triangle: the biggest side is opposite the biggest angle and vice versa the smallest side is opposite the smallest angle and vice versa. an isosceles triangle is one that has 2 equal side lengths. the opposite angles of these two identical sides are similarly equal. in a triangle, the sum of any of the two sides. In a triangle, the angle opposite the longer side is the larger angle. example 1: compare the lengths of the sides of the following triangle. solution: step 1: we need to find the size of the third angle. the sum of all the angles in any triangle is 180º. ∠a ∠b ∠c = 180°. ⇒ ∠a 30° 65° = 180°. ⇒ ∠a = 180° 95°.

Angle Side Relationship In Triangles Youtube Angle side relationships in a triangle: the biggest side is opposite the biggest angle and vice versa the smallest side is opposite the smallest angle and vice versa. an isosceles triangle is one that has 2 equal side lengths. the opposite angles of these two identical sides are similarly equal. in a triangle, the sum of any of the two sides. In a triangle, the angle opposite the longer side is the larger angle. example 1: compare the lengths of the sides of the following triangle. solution: step 1: we need to find the size of the third angle. the sum of all the angles in any triangle is 180º. ∠a ∠b ∠c = 180°. ⇒ ∠a 30° 65° = 180°. ⇒ ∠a = 180° 95°.
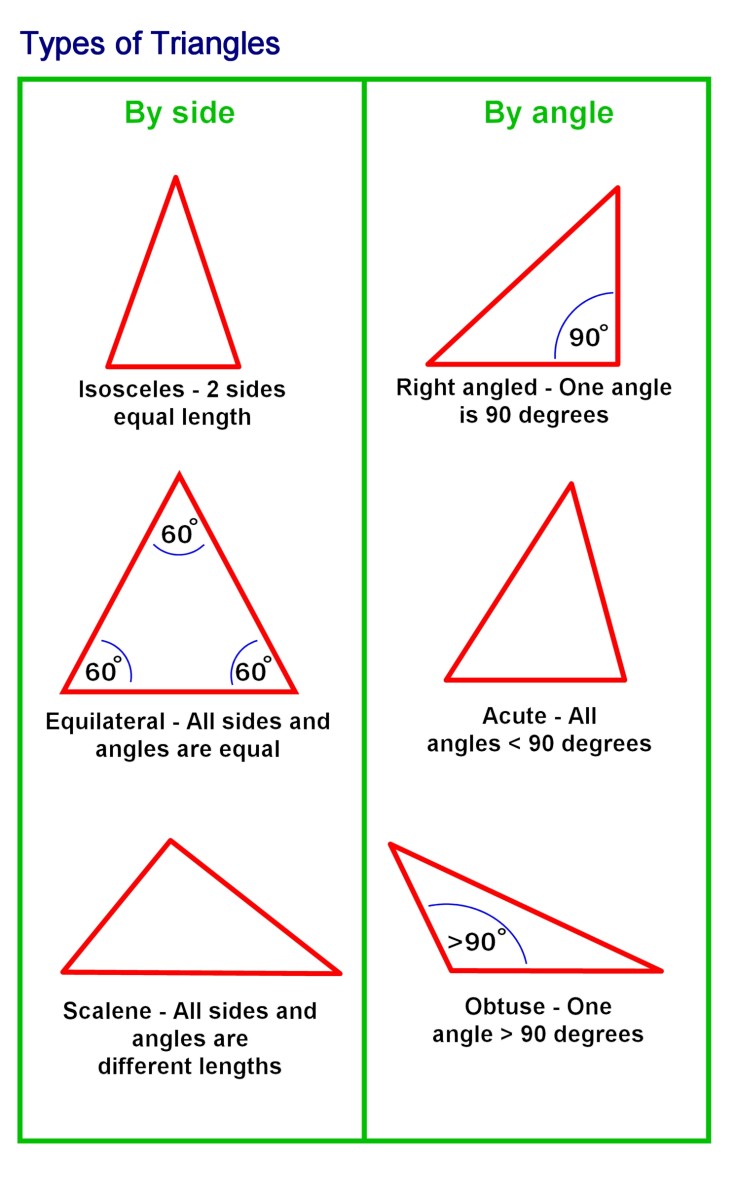
How To Calculate The Sides And Angles Of Triangles Owlcation

Comments are closed.