Triangle Law Of Vector Addition Dont Memorise

Triangle Law Of Vector Addition Don T Memorise Youtube 🎯neet 2024 paper solutions with neet answer key: watch?v=fwxyzubp4m0&list=plmdfyqyshrjc4oswbsticoypgl0tjtgon&index=1📅🆓neet rank &. Triangle law of vector addition is one of the vector addition laws. vector addition is defined as the geometrical sum of two or more vectors as they do not follow regular laws of algebra. the resultant vector is known as the composition of a vector. there are a few conditions that are applicable for any vector addition, they are:.
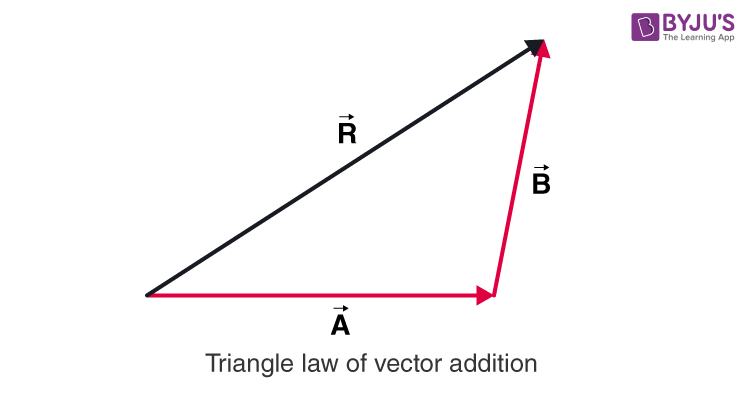
Triangle Law Of Vector Addition Formula And Derivation Hence, we have proved the formulas for the triangle law of vector addition. important notes on triangle law of vector addition. triangle law of vector addition is used to find the sum of two vectors when the head of the first vector is joined to the tail of the second vector. magnitude of the resultant sum vector r: r = √(p 2 2pq cos θ q 2). Solved examples on triangle law of vector addition. example 1: two vectors p and q have magnitudes of 9 units and 16 units and make an angle of 30° with each other. using triangle law of vector addition, find the magnitude and direction of resultant vector. solution: according to the triangle law of vector addition |r| = √(a 2 b 2 2abcosθ). The triangle law of vector addition states that if two vectors are represented as two sides of a triangle taken in the same order, then their resultant vector is represented in magnitude and direction by the third side of the triangle. let's consider two vectors p → and q →. according to the triangle law, if we draw these vectors as two. Derivation of the law. consider two vectors p and q acting on a body and represented both in magnitude and direction by sides oa and ab respectively of a triangle oab. let θ be the angle between p and q. let r be the resultant of vectors p and q. then, according to triangle law of vector addition, side ob represents the resultant of p and q.

Triangle Law Of Vector Addition Formula Proof Examples Statement The triangle law of vector addition states that if two vectors are represented as two sides of a triangle taken in the same order, then their resultant vector is represented in magnitude and direction by the third side of the triangle. let's consider two vectors p → and q →. according to the triangle law, if we draw these vectors as two. Derivation of the law. consider two vectors p and q acting on a body and represented both in magnitude and direction by sides oa and ab respectively of a triangle oab. let θ be the angle between p and q. let r be the resultant of vectors p and q. then, according to triangle law of vector addition, side ob represents the resultant of p and q. Triangle rule of vector addition. all methods of vector addition are ultimately based on the tip to tail method discussed in a one dimensional context in subsection 2.2.1. there are two ways to draw or visualize adding vectors in two or three dimensions, the triangle rule and parallelogram rule. both are equivalent. Now from e, draw a line segment → ef equal and parallel to → cd, which represents the vector →b. line segment → of obtained by joining o and f represents the sum of vectors →a and →b. i.e. → oe → ef = → of. or →a →b = → of. this method of addition of two vectors is called triangle law of addition of vectors.

Triangle Law Of Vector Addition Triangle rule of vector addition. all methods of vector addition are ultimately based on the tip to tail method discussed in a one dimensional context in subsection 2.2.1. there are two ways to draw or visualize adding vectors in two or three dimensions, the triangle rule and parallelogram rule. both are equivalent. Now from e, draw a line segment → ef equal and parallel to → cd, which represents the vector →b. line segment → of obtained by joining o and f represents the sum of vectors →a and →b. i.e. → oe → ef = → of. or →a →b = → of. this method of addition of two vectors is called triangle law of addition of vectors.

Comments are closed.