Three Proofs Of The Pythagorean Theorem
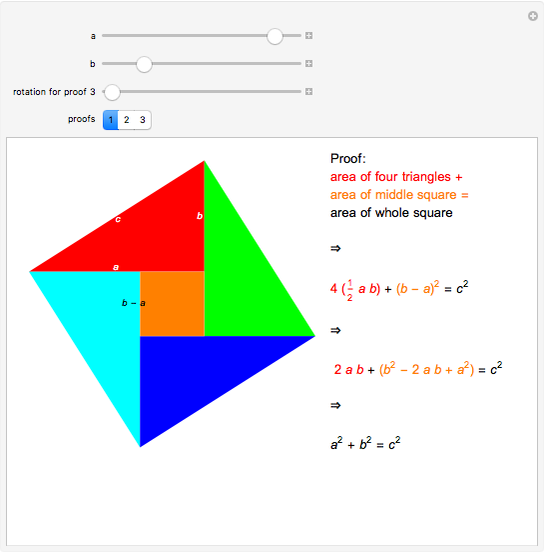
Three Proofs Of The Pythagorean Theorem Wolfram Demonstrations Project Pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see two squares inside the. Pertinent to that proof is a page "extra geometric" proofs of the pythagorean theorem by scott brodie. proof #30. this proof i found in r. nelsen's sequel proofs without words ii. (it's due to poo sung park and was originally published in mathematics magazine, dec 1999). starting with one of the sides of a right triangle, construct 4 congruent.
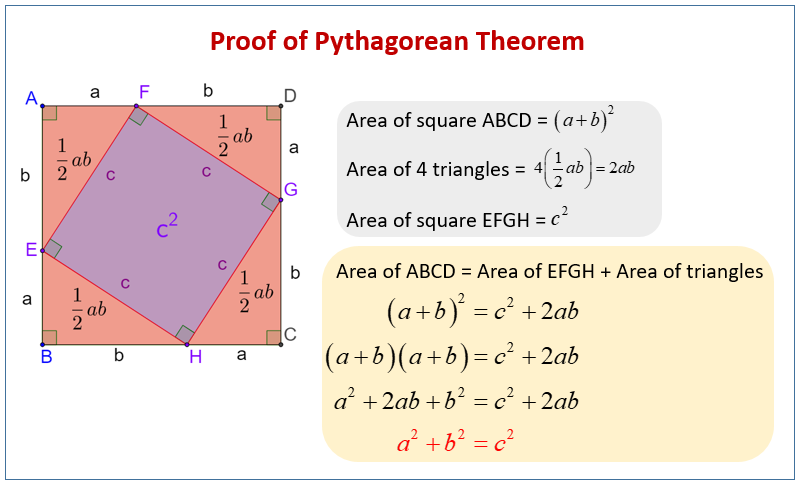
Proving The Pythagorean Theorem Math Liberty In mathematics, the pythagorean theorem or pythagoras' theorem is a fundamental relation in euclidean geometry between the three sides of a right triangle. it states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. My favorite proof of the pythagorean theorem is a special case of this picture proof of the law of cosines: drop three perpendiculars and let the definition of cosine give the lengths of the sub divided segments. then, observe that like colored rectangles have the same area (computed in slightly different ways) and the result follows immediately. What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. The pythagorean theorem states that if a triangle has one right angle, then the square of the longest side, called the hypotenuse, is equal to the sum of the squares of the lengths of the two shorter sides, called the legs. so if a a and b b are the lengths of the legs, and c c is the length of the hypotenuse, then a^2 b^2=c^2 a2 b2 = c2.

How To Prove The Pythagorean Theorem 10 Steps With Pictures What is the pythagorean theorem? you can learn all about the pythagorean theorem, but here is a quick summary: the pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2. proof of the pythagorean theorem using algebra. The pythagorean theorem states that if a triangle has one right angle, then the square of the longest side, called the hypotenuse, is equal to the sum of the squares of the lengths of the two shorter sides, called the legs. so if a a and b b are the lengths of the legs, and c c is the length of the hypotenuse, then a^2 b^2=c^2 a2 b2 = c2. A great many different proofs and extensions of the pythagorean theorem have been invented. taking extensions first, euclid himself showed in a theorem praised in antiquity that any symmetrical regular figures drawn on the sides of a right triangle satisfy the pythagorean relationship: the figure drawn on the hypotenuse has an area equal to the sum of the areas of the figures drawn on the legs. Pythagorean theorem – proofs. as far as proofs are concerned, it's difficult to beat the pythagorean theorem. it has literally hundreds of proofs. of course, we won't be discussing all of them in this tutorial. but let's look at a couple of them. proof 1 (using rearrangement) we start with a right triangle and a square shown in the figure below.
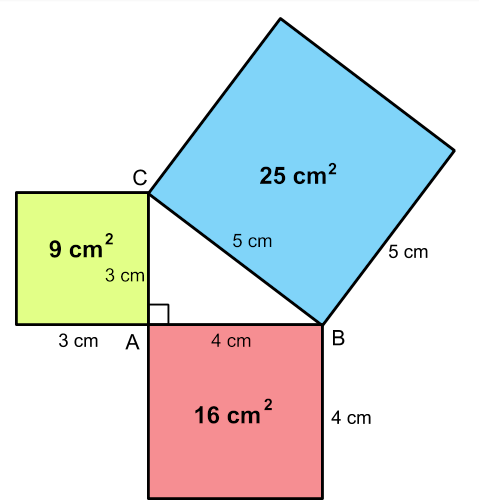
The Pythagorean Theorem Math Tutor Free Math For All A great many different proofs and extensions of the pythagorean theorem have been invented. taking extensions first, euclid himself showed in a theorem praised in antiquity that any symmetrical regular figures drawn on the sides of a right triangle satisfy the pythagorean relationship: the figure drawn on the hypotenuse has an area equal to the sum of the areas of the figures drawn on the legs. Pythagorean theorem – proofs. as far as proofs are concerned, it's difficult to beat the pythagorean theorem. it has literally hundreds of proofs. of course, we won't be discussing all of them in this tutorial. but let's look at a couple of them. proof 1 (using rearrangement) we start with a right triangle and a square shown in the figure below.

Pythagoras Theorem Explained
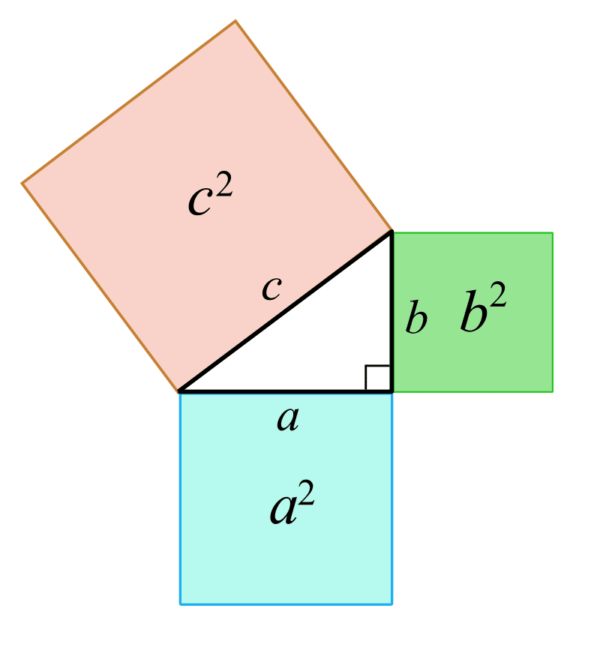
Pythagoras Theorem Pythagorean Formula Proof Examples Full

Comments are closed.