Theta Making Precalculus Fun

Theta Making Precalculus Fun Theta rational functions: division, multiplication, addition subtraction coordinates: polar, cartesian rectangular complex converting polar to cartesian and back complex conjugates rational root theorem domain and range function notation interval notation polynomials standard form of a polynomial end behavior of graphs. Theta; rational functions: division, multiplication, addition subtraction; coordinates: polar, cartesian rectangular complex; converting polar to cartesian and back; complex conjugates; rational root theorem; domain and range; function notation; interval notation; polynomials; standard form of a polynomial; end behavior of graphs; distance.

Precalculus Chapter 4 2 Exercises 41 54 Solve For Theta Find The Fun. tolerable. chris is a stanford educated tutor with over 10 years experience tutoring pre calculus to students of all abilities, from students struggling to get from a c to a b, to go getters trying to move an a up to an a, to struggling students just hoping to pass. in that time he got a lot of experience learning how to explain this. Since the trigonometric functions repeat every 2π 2 π radians (360∘ 360 ∘), we get, for example, the following graph of the function y = sin x y = sin x for x x in the interval [−2π, 2π] [− 2 π, 2 π]: figure 5.1.4 5.1. 4 graph of y = sin x y = sin x. to graph the cosine function, we could again use the unit circle idea (using the. We will begin with the pythagorean identities, which are equations involving trigonometric functions based on the properties of a right triangle. we have already seen and used the first of these identifies, but now we will also use additional identities. pythagorean identities. sin2θ cos2θ = 1 sin 2 θ cos 2 θ = 1. Answer: the polar equation of a rose curve is either r = acosnθ or r = asinnθ. the number of rose petals will be n or 2n according as n is an odd or an even integer. see explanation. explanation: having seen that there were more than 1 k viewers in a day, i now add more. the 2 d polar coordinates p (r,θ), r = √x2 y2 ≥ 0.

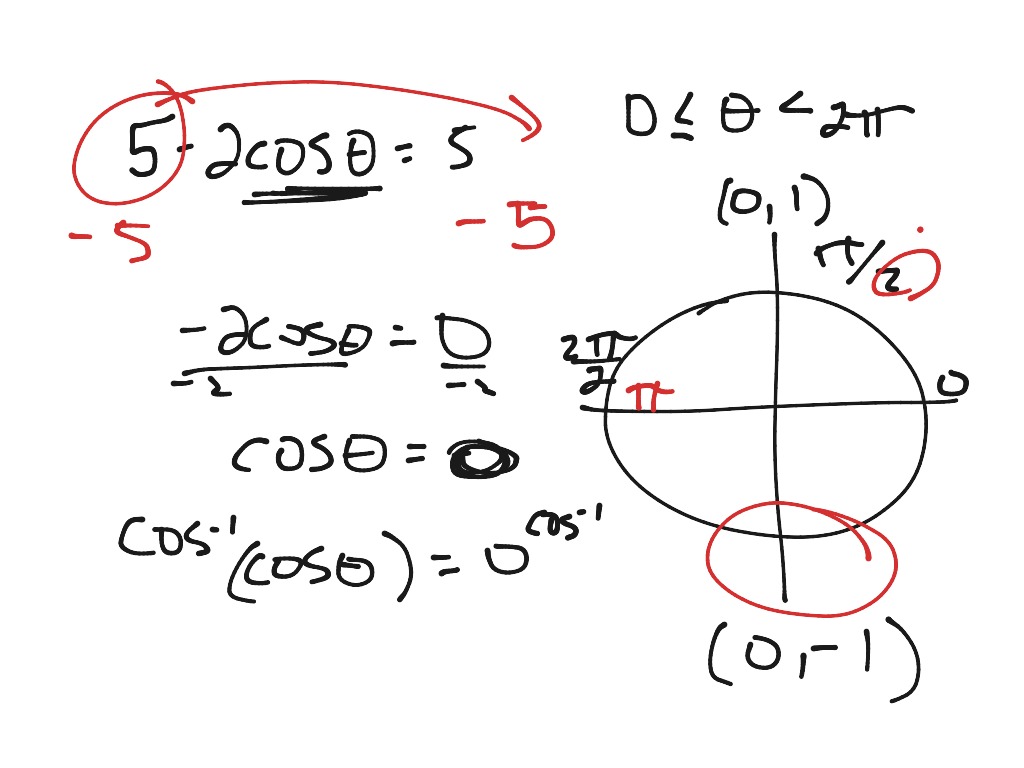
Solving For Theta Math Precalculus Trigonometry Equations And We will begin with the pythagorean identities, which are equations involving trigonometric functions based on the properties of a right triangle. we have already seen and used the first of these identifies, but now we will also use additional identities. pythagorean identities. sin2θ cos2θ = 1 sin 2 θ cos 2 θ = 1. Answer: the polar equation of a rose curve is either r = acosnθ or r = asinnθ. the number of rose petals will be n or 2n according as n is an odd or an even integer. see explanation. explanation: having seen that there were more than 1 k viewers in a day, i now add more. the 2 d polar coordinates p (r,θ), r = √x2 y2 ≥ 0. A vector is specified by its components along the coordinate axes in a particular coordinate system. a vector projection of a vector a along some direction is the component of the vector along that direction. if a makes an angle θ with the direction in which we are to find it's projection and it's magnitude a, the projection is given as acosθ. An angle’s reference angle is the measure of the smallest, positive, acute angle t formed by the terminal side of the angle t and the horizontal axis. thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. see figure 1 for examples of reference angles for.

Precalculus Trigonometry Trig Identities 46 Of 57 Solve 3sin Theta A vector is specified by its components along the coordinate axes in a particular coordinate system. a vector projection of a vector a along some direction is the component of the vector along that direction. if a makes an angle θ with the direction in which we are to find it's projection and it's magnitude a, the projection is given as acosθ. An angle’s reference angle is the measure of the smallest, positive, acute angle t formed by the terminal side of the angle t and the horizontal axis. thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. see figure 1 for examples of reference angles for.