Thermodynamics Specific Heats Cv Cp In 12 Minutes

Thermodynamics Specific Heats Cv Cp In 12 Minutes Youtube Specific heat at constant volumespecific heat at constant pressureheat capacityenthalpyinternal energycv and cptables and polynomial fits0:00 general specifi. Specific heats – cp and cv. thermodynamics is a branch of physics which deals with the energy and work of a system. thermodynamics deals only with the large scale response of a system which we can observe and measure in experiments. like the wright brothers, we are most interested in thermodynamics for the role it plays in engine design.

Cp Cv Relations In Thermodynamics Specific Heats Relations Derivation From the definition of enthalpy: h = e p * v. where h in the specific enthalpy, p is the pressure, v is the specific volume, and e is the specific internal energy. during a process, the values of these variables change. let's denote the change by the greek letter delta which looks like a triangle. so "delta h" means the change of "h" from. The relationship between c p and c v for an ideal gas. from the equation q = n c ∆t, we can say: at constant pressure p, we have. qp = n cp∆t. this value is equal to the change in enthalpy, that is, qp = n cp∆t = ∆h. similarly, at constant volume v, we have. qv = n cv∆t. this value is equal to the change in internal energy, that is,. The specific heat at constant pressure for an ideal gas is given as (∂ h ∂ t)v = cp = cv r. the heat capacity ratio (or adiabatic index ) is the ratio of the heat capacity at constant pressure to heat capacity at constant volume. calorimetry is used to measure amounts of heat transferred to or from a substance. 3) in general, u is a function of two properties of the system (as is h), however, if u=u (t) only and h=h (t) only then du=cvdt and dh=cpdt. if this gas also obeys pv=rt (a thermally perfect gas), then the gas is called an ideal gas. many of the gases we deal with behave this way. 4) cv and cp allow us to relate changes in h and u to changes in t.

Specific Heat Capacities Of Gas Cp And Cv First Law Of The specific heat at constant pressure for an ideal gas is given as (∂ h ∂ t)v = cp = cv r. the heat capacity ratio (or adiabatic index ) is the ratio of the heat capacity at constant pressure to heat capacity at constant volume. calorimetry is used to measure amounts of heat transferred to or from a substance. 3) in general, u is a function of two properties of the system (as is h), however, if u=u (t) only and h=h (t) only then du=cvdt and dh=cpdt. if this gas also obeys pv=rt (a thermally perfect gas), then the gas is called an ideal gas. many of the gases we deal with behave this way. 4) cv and cp allow us to relate changes in h and u to changes in t. We have. cp = cv r. (one mole of any ideal gas) for a monatomic ideal gas, cp = cv r = 3 2r r = 5 2r. (one mole of a monatomic ideal gas) the heat capacity functions have a pivotal role in thermodynamics. we consider many of their properties further in the next section and in later chapters (particularly § 10 9 and § 10 10.). We can therefore use our definition of specific heat from equation (2.4) to define the specific heat for a constant volume process, the specific heat at constant pressure. if we write , and consider a constant pressure process, we can perform a similar derivation to the one above and show that.
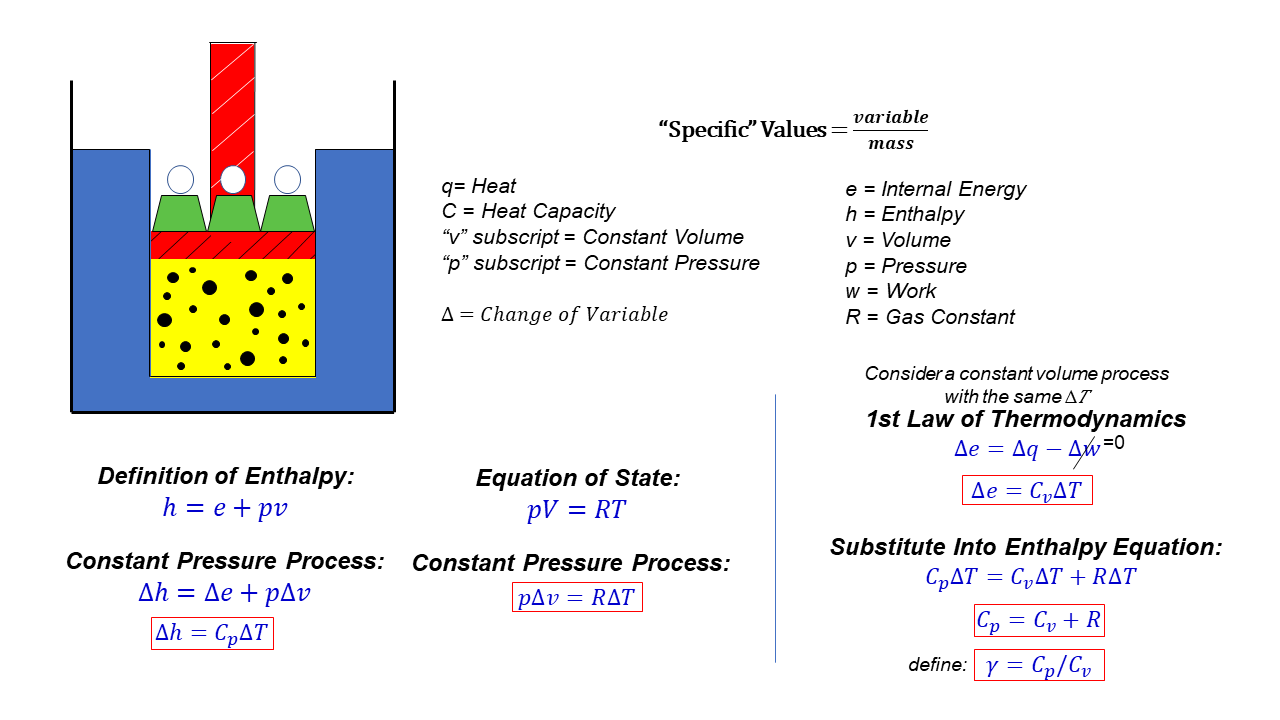
Specific Heats Cp And Cv Glenn Research Center Nasa We have. cp = cv r. (one mole of any ideal gas) for a monatomic ideal gas, cp = cv r = 3 2r r = 5 2r. (one mole of a monatomic ideal gas) the heat capacity functions have a pivotal role in thermodynamics. we consider many of their properties further in the next section and in later chapters (particularly § 10 9 and § 10 10.). We can therefore use our definition of specific heat from equation (2.4) to define the specific heat for a constant volume process, the specific heat at constant pressure. if we write , and consider a constant pressure process, we can perform a similar derivation to the one above and show that.

Specific Heats

Thermodynamics Class 11 To Prove Cp Cv R Molar Specific Heats Of

Comments are closed.