Theorem 6 3 Class 9 If A Transversal Intersects Two Lines Such That A

Theorem 6 3 Class 9 If A Transversal Intersects Two Lines Such That A Theorem 6.3 : if a transversal intersects two lines, such that a pair of alternate interior angles is equal, then the two lines are parallel. given : two lines ab and cd. and transversal ps intersecting ab at q and cd at r, such that alternate interior angles are equal. i.e, bqr = cr. To prove theorem 6.3, we need to show that if a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel. here is the step by step solution: 1. draw the diagram : draw two lines, let’s call them line ab and line cd.

Example 5 If A Transversal Intersects Two Lines Such That Now use the converse of the corresponding angle theorem to prove two lines parallel. complete step by step answer: here we have to prove that if a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. let us represent this situation diagrammatically. Theorem:6.2 if a transversal intersects two parallel lines,then each pair of alternate interior angles is equal.ncert maths class 9 cbse board#mathsclass9cha. Or angle 2; the interior opposite angles are abc and acb. for exter. gles are bac and acb.triangles theorem 1:statement: if a side of a triangle is produced, the exterior angle so f. ual to the sum of the interior opposite angles.given: in triangle, abc , sid. bc is produced to d and acdis the exterior a. How to prove theorem 6.3 in class 9 maths? theorem if a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel. please prove it. how to prove theorem 6.3 in class 9 maths? theorem if a transversal intersects two lines such that a pair of alternate interior angles is equal.

Theorem 6 3 Class 9 Maths Explanation With Proof Remedial Classes Or angle 2; the interior opposite angles are abc and acb. for exter. gles are bac and acb.triangles theorem 1:statement: if a side of a triangle is produced, the exterior angle so f. ual to the sum of the interior opposite angles.given: in triangle, abc , sid. bc is produced to d and acdis the exterior a. How to prove theorem 6.3 in class 9 maths? theorem if a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel. please prove it. how to prove theorem 6.3 in class 9 maths? theorem if a transversal intersects two lines such that a pair of alternate interior angles is equal. Ncert exemplar class 9 maths exercise 6.2 sample problem 2. a transversal intersects two lines in such a way that the two interior angles on the same side of the transversal are equal. will the two lines always be parallel? give reason for your answer. summary: a transversal intersects two lines in such a way that the two interior angles on the. The transversal ad intersects the two lines pq and rs at points b and c respectively. be is the bisector of abq and cf is the bisector of bcs. as, be is the bisector of abq, then, abe= 1 2 abq in the same way, bcf=1 2 bcs since be and cf are parallel and ad is the transversal, therefore, by corresponding angle axiom, abe= bcf 1 2 abq= 1 2 bcs abq= bcs therefore, by the converse of.

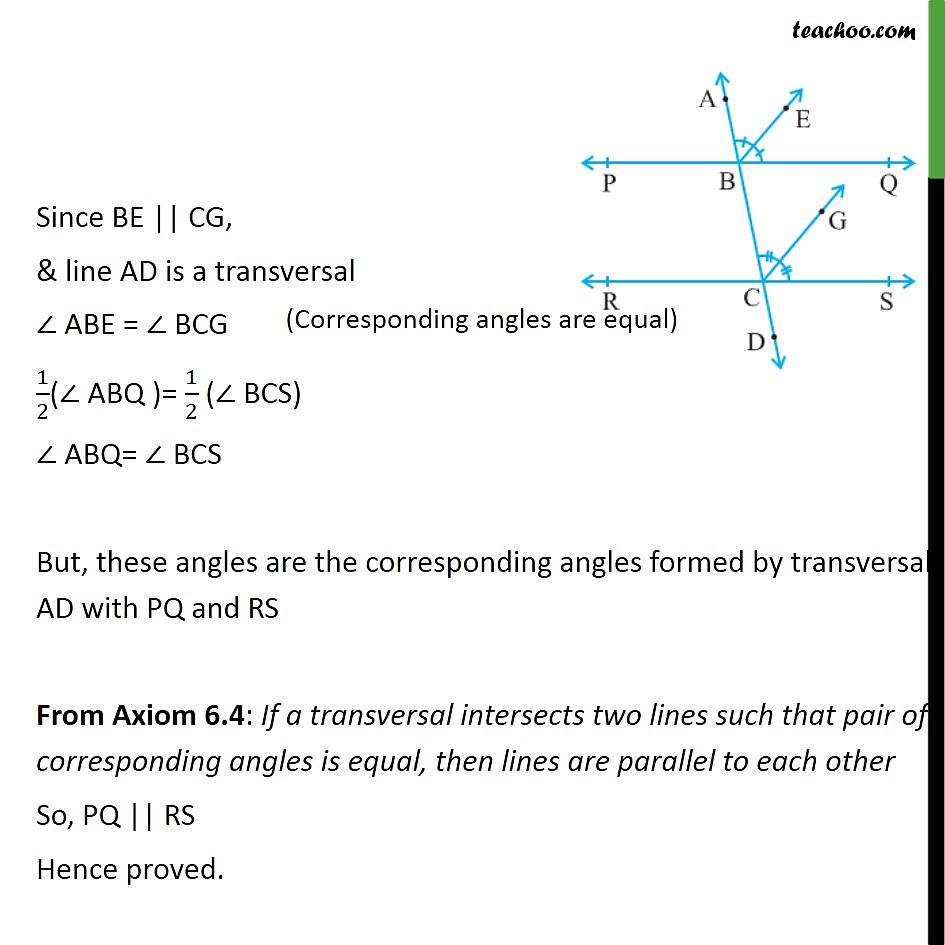
Example 5 If A Transversal Intersects Two Lines Such That Ncert exemplar class 9 maths exercise 6.2 sample problem 2. a transversal intersects two lines in such a way that the two interior angles on the same side of the transversal are equal. will the two lines always be parallel? give reason for your answer. summary: a transversal intersects two lines in such a way that the two interior angles on the. The transversal ad intersects the two lines pq and rs at points b and c respectively. be is the bisector of abq and cf is the bisector of bcs. as, be is the bisector of abq, then, abe= 1 2 abq in the same way, bcf=1 2 bcs since be and cf are parallel and ad is the transversal, therefore, by corresponding angle axiom, abe= bcf 1 2 abq= 1 2 bcs abq= bcs therefore, by the converse of.

Theorem 6 3 Class 9 If Alternate Angles Are Equal Lines Parallel

Heya Prove The Theorem 6 3 If A Transversal Intersects Two Lines