The Standard Normal Distribution Examples Explanations Uses

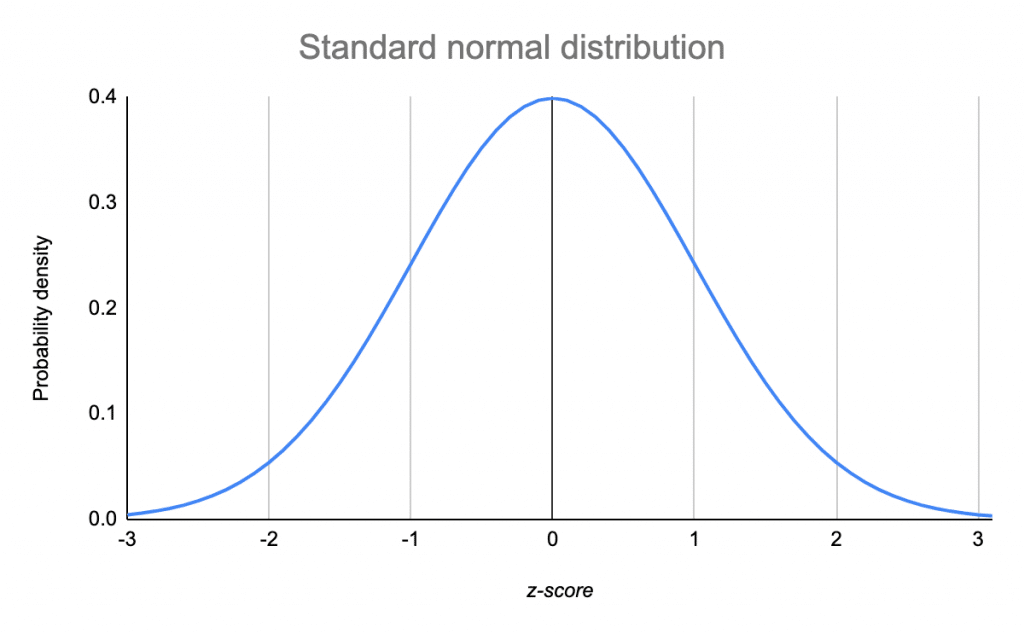
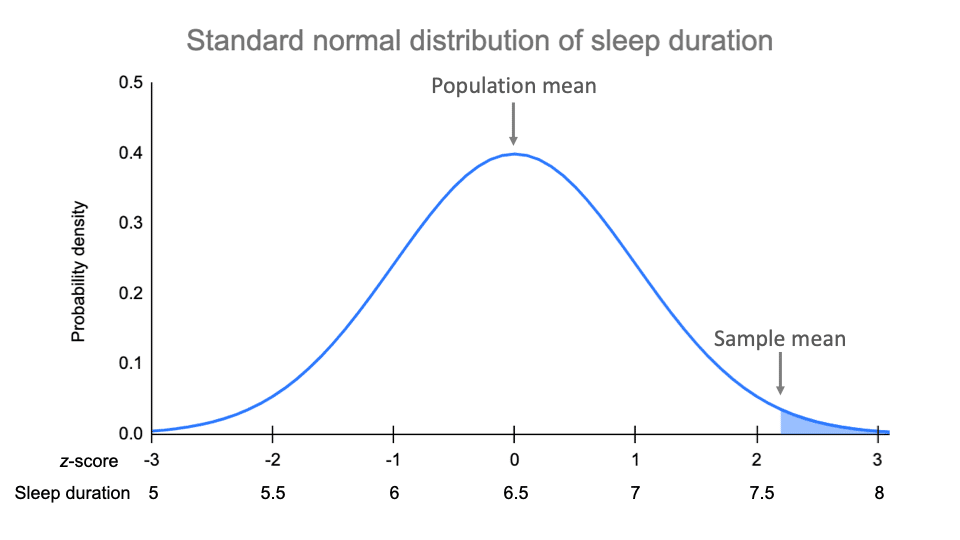
The Standard Normal Distribution Examples Explanations Uses X – m = 1380 − 1150 = 230. step 2: divide the difference by the standard deviation. sd = 150. z = 230 ÷ 150 = 1.53. the z score for a value of 1380 is 1.53. that means 1380 is 1.53 standard deviations from the mean of your distribution. next, we can find the probability of this score using a z table. Height, birth weight, reading ability, job satisfaction, or sat scores are just a few examples of such variables. because normally distributed variables are so common, many statistical tests are designed for normally distributed populations. understanding the properties of normal distributions means you can use inferential statistics to compare.

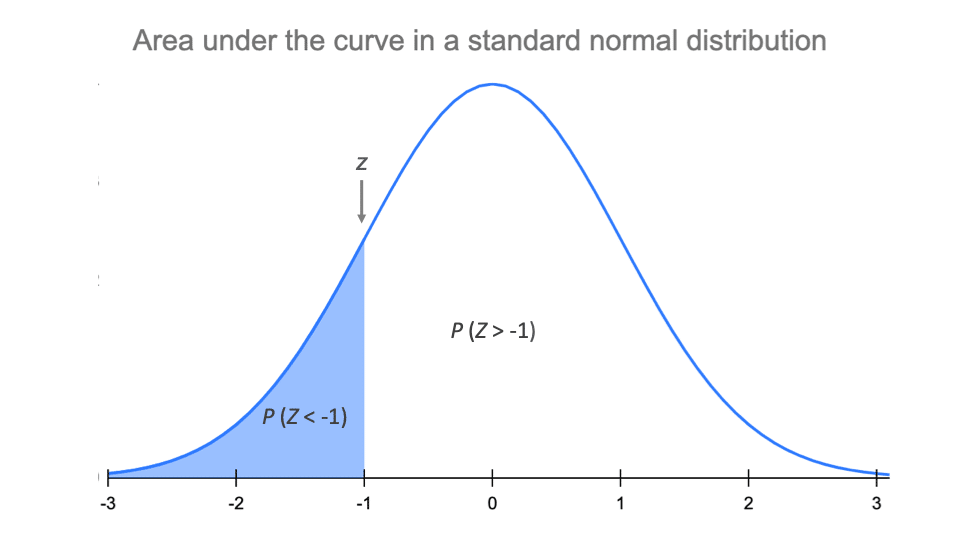
The Standard Normal Distribution Examples Explanations Uses Example 1: birthweight of babies. it’s well documented that the birthweight of newborn babies is normally distributed with a mean of about 7.5 pounds. the histogram of the birthweight of newborn babies in the u.s. displays a bell shape that is typically of the normal distribution:. Standard normal distribution and standard scores. as we’ve seen above, the normal distribution has many different shapes depending on the parameter values. however, the standard normal distribution is a special case of the normal distribution where the mean is zero and the standard deviation is 1. The standard normal distribution allows very different sets of data to be compared. once the data is standardized, it will follow the 68 95 99.7 rule. this allows comparisons between the math test. The standard deviation is 0.15m, so: 0.45m 0.15m = 3 standard deviations. so to convert a value to a standard score ("z score"): first subtract the mean, then divide by the standard deviation. and doing that is called "standardizing": we can take any normal distribution and convert it to the standard normal distribution.

The Standard Normal Distribution Examples Explanations Uses The standard normal distribution allows very different sets of data to be compared. once the data is standardized, it will follow the 68 95 99.7 rule. this allows comparisons between the math test. The standard deviation is 0.15m, so: 0.45m 0.15m = 3 standard deviations. so to convert a value to a standard score ("z score"): first subtract the mean, then divide by the standard deviation. and doing that is called "standardizing": we can take any normal distribution and convert it to the standard normal distribution. A normal distribution is determined by two parameters the mean and the variance. a normal distribution with a mean of 0 and a standard deviation of 1 is called a standard normal distribution. figure 1. a standard normal distribution (snd). this is the distribution that is used to construct tables of the normal distribution. X = μ (z)(σ) = 5 (3)(2) = 11. the z score is three. since the mean for the standard normal distribution is zero and the standard deviation is one, then the transformation in equation 6.2.1 produces the distribution z ∼ n(0, 1). the value x comes from a normal distribution with mean μ and standard deviation σ.

The Standard Normal Distribution Examples Explanations Uses A normal distribution is determined by two parameters the mean and the variance. a normal distribution with a mean of 0 and a standard deviation of 1 is called a standard normal distribution. figure 1. a standard normal distribution (snd). this is the distribution that is used to construct tables of the normal distribution. X = μ (z)(σ) = 5 (3)(2) = 11. the z score is three. since the mean for the standard normal distribution is zero and the standard deviation is one, then the transformation in equation 6.2.1 produces the distribution z ∼ n(0, 1). the value x comes from a normal distribution with mean μ and standard deviation σ.