The Power Rule For Derivatives
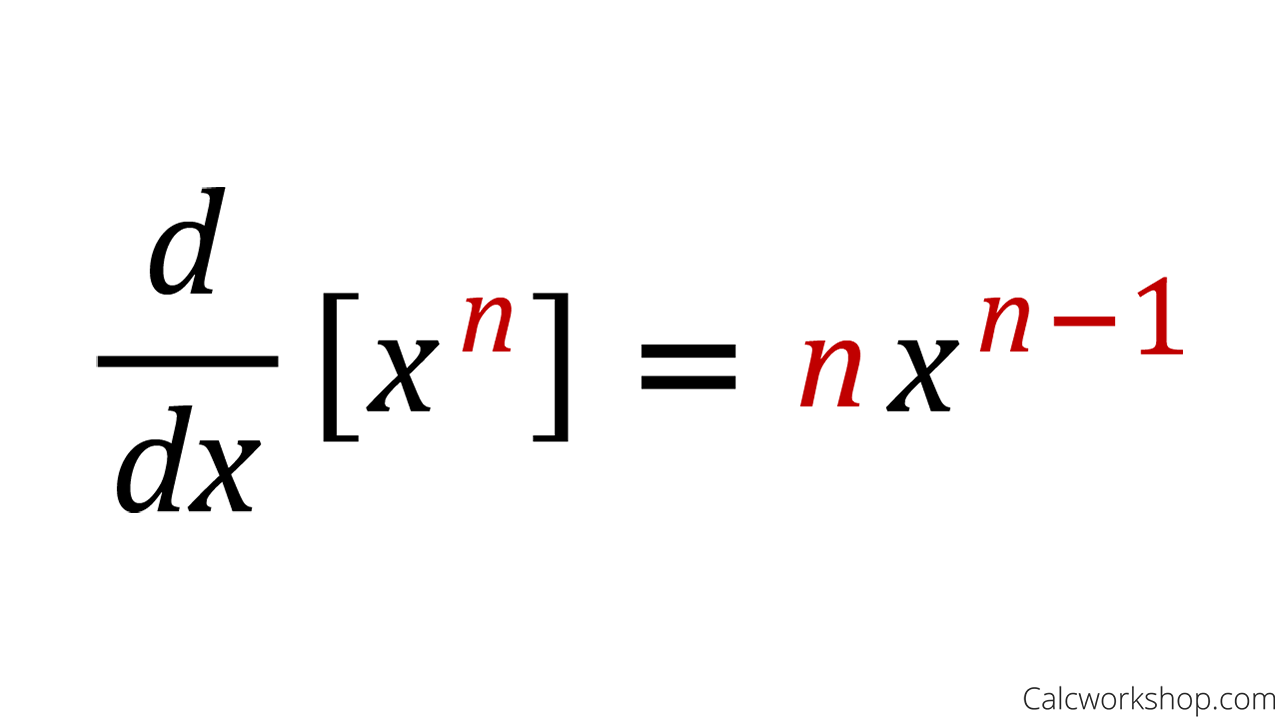
Power Rule How To W 9 Step By Step Examples Learn how to use the power rule to find derivatives of polynomials, functions with negative exponents, and functions with radicals. see examples, definitions, and explanations with steps. Learn how to differentiate algebraic expressions with power using the power rule formula d (x n) dx = nx n 1. see the proof of the formula using mathematical induction and binomial theorem, and explore its applications in calculus.

The Power Rule For Derivatives Youtube This page titled 2.4: power and sum rules for derivatives is shared under a cc by 3.0 license and was authored, remixed, and or curated by shana calaway, dale hoffman, & david lippman (the opentextbookstore) via source content that was edited to the style and standards of the libretexts platform. The power rule tells us how to find the derivative of any expression in the form x n : d d x [x n] = n ⋅ x n − 1. the ap calculus course doesn't require knowing the proof of this rule, but we believe that as long as a proof is accessible, there's always something to learn from it. in general, it's always good to require some kind of proof. Calculus. in calculus, the power rule is used to differentiate functions of the form , whenever is a real number. since differentiation is a linear operation on the space of differentiable functions, polynomials can also be differentiated using this rule. the power rule underlies the taylor series as it relates a power series with a function's. To better understand the sequence in which the differentiation rules are applied, we use leibniz notation throughout the solution: f′ (x) = d dx(2x5 7) = d dx(2x5) d dx(7) apply the sum rule. = 2 d dx(x5) d dx(7) apply the constant multiple rule. = 2(5x4) 0 apply the power rule and the constant rule. = 10x4 simplify.
Differentiation Rules The Power Rule Math Concepts Explained Calculus. in calculus, the power rule is used to differentiate functions of the form , whenever is a real number. since differentiation is a linear operation on the space of differentiable functions, polynomials can also be differentiated using this rule. the power rule underlies the taylor series as it relates a power series with a function's. To better understand the sequence in which the differentiation rules are applied, we use leibniz notation throughout the solution: f′ (x) = d dx(2x5 7) = d dx(2x5) d dx(7) apply the sum rule. = 2 d dx(x5) d dx(7) apply the constant multiple rule. = 2(5x4) 0 apply the power rule and the constant rule. = 10x4 simplify. Foundational rules. power rule: for functions like xⁿ, the derivative is nxⁿ⁻¹. for example, the derivative of x³ is 3x². constant rule: the derivative of any constant (like 5, 2, or π) is always 0. a constant doesn’t change, so its rate of change is zero. constant multiple rule: for a function multiplied by a constant (cf (x. Learn how to use the power rule to find the slope of polynomial and other functions with exponents. see examples, video tutorial, and differentiation rules for constants, sums, and differences.

The Power Rule For Derivatives Youtube Foundational rules. power rule: for functions like xⁿ, the derivative is nxⁿ⁻¹. for example, the derivative of x³ is 3x². constant rule: the derivative of any constant (like 5, 2, or π) is always 0. a constant doesn’t change, so its rate of change is zero. constant multiple rule: for a function multiplied by a constant (cf (x. Learn how to use the power rule to find the slope of polynomial and other functions with exponents. see examples, video tutorial, and differentiation rules for constants, sums, and differences.

Comments are closed.