The Least Squares Regression Line
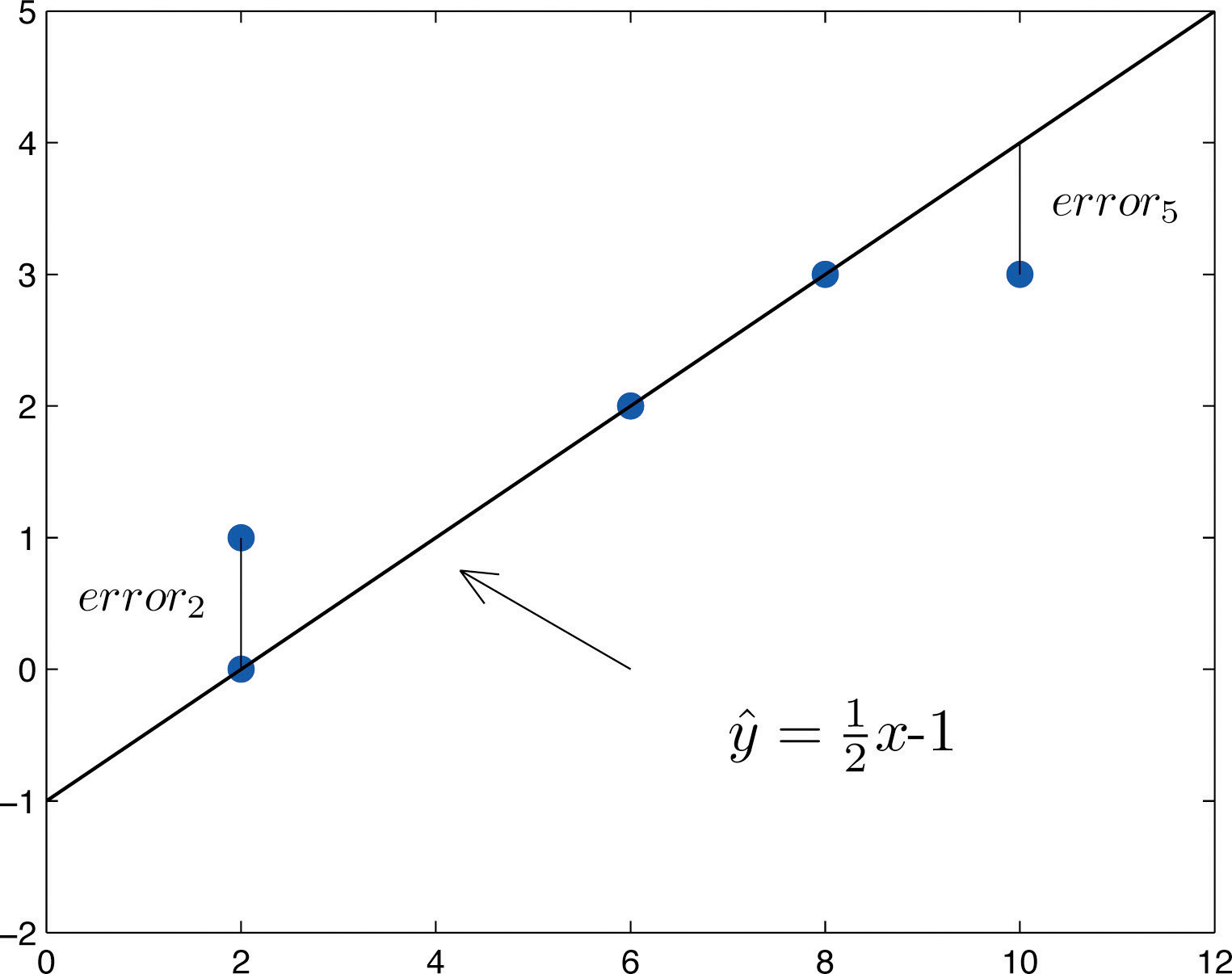
The Least Squares Regression Line Learn how to calculate the equation of a line that best fits a set of points using the least squares method. see examples, formulas, graphs and an interactive calculator. A least squares regression line represents the relationship between variables in a scatterplot. the procedure fits the line to the data points in a way that minimizes the sum of the squared vertical distances between the line and the points. it is also known as a line of best fit or a trend line.
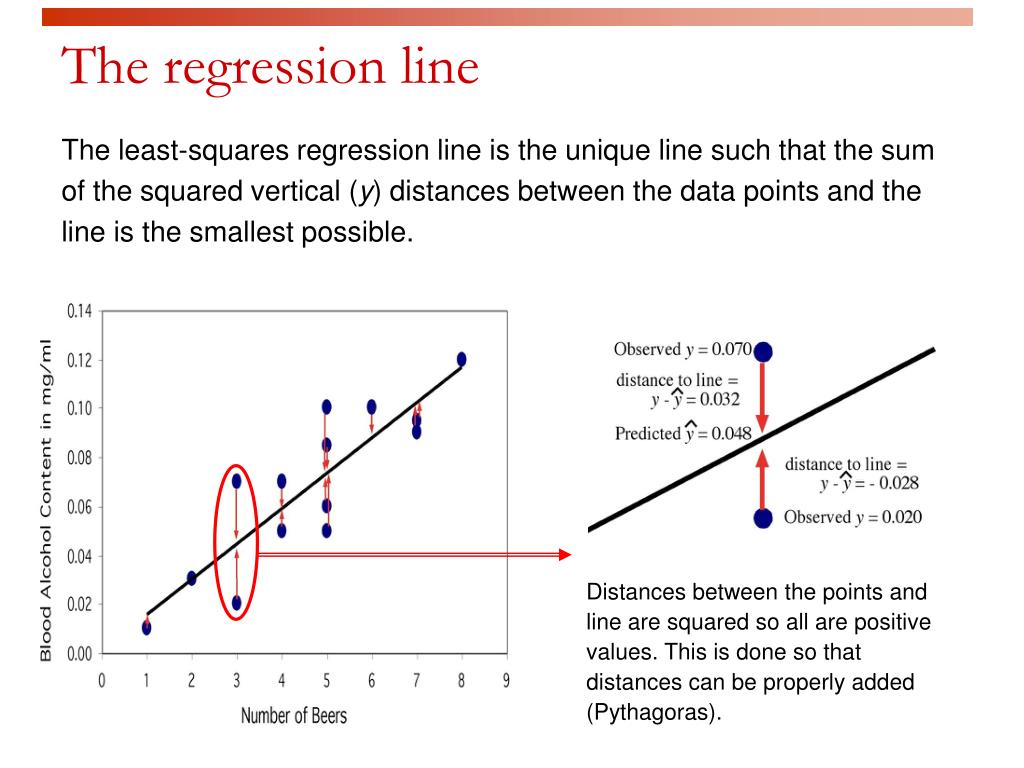
Ppt Least Squares Regression Powerpoint Presentation Free Download The least squares regression line for these data is. ˆy = 0.34375x − 0.125. the computations for measuring how well it fits the sample data are given in table 10.4.2. the sum of the squared errors is the sum of the numbers in the last column, which is 0.75. Learn how to find the line of best fit for multiple data points using the least squares method. use the calculator to estimate the slope, intercept, correlation coefficient and error of the regression line. Least squares regression lines. residuals. residual plots. scatterplots are a way for us to visually display a relationship between two quantitative variables, typically written in the form (x,y), where x is the explanatory or independent variable, and y is the response or dependent variable. When fitting a least squares line, we generally require. linearity. the data should show a linear trend. if there is a nonlinear trend (e.g. left panel of figure 7.3.2 7.3. 2. ), an advanced regression method from another book or later course should be applied. nearly normal residuals.

Least Squares Regression Line Andymath Least squares regression lines. residuals. residual plots. scatterplots are a way for us to visually display a relationship between two quantitative variables, typically written in the form (x,y), where x is the explanatory or independent variable, and y is the response or dependent variable. When fitting a least squares line, we generally require. linearity. the data should show a linear trend. if there is a nonlinear trend (e.g. left panel of figure 7.3.2 7.3. 2. ), an advanced regression method from another book or later course should be applied. nearly normal residuals. In linear regression, a residual is the difference between the actual value and the value predicted by the model (y ŷ) for any given point. a least squares regression model minimizes the sum of the squared residuals. Least squares is a method to apply linear regression. it helps us predict results based on an existing set of data as well as clear anomalies in our data. anomalies are values that are too good, or bad, to be true or that represent rare cases.
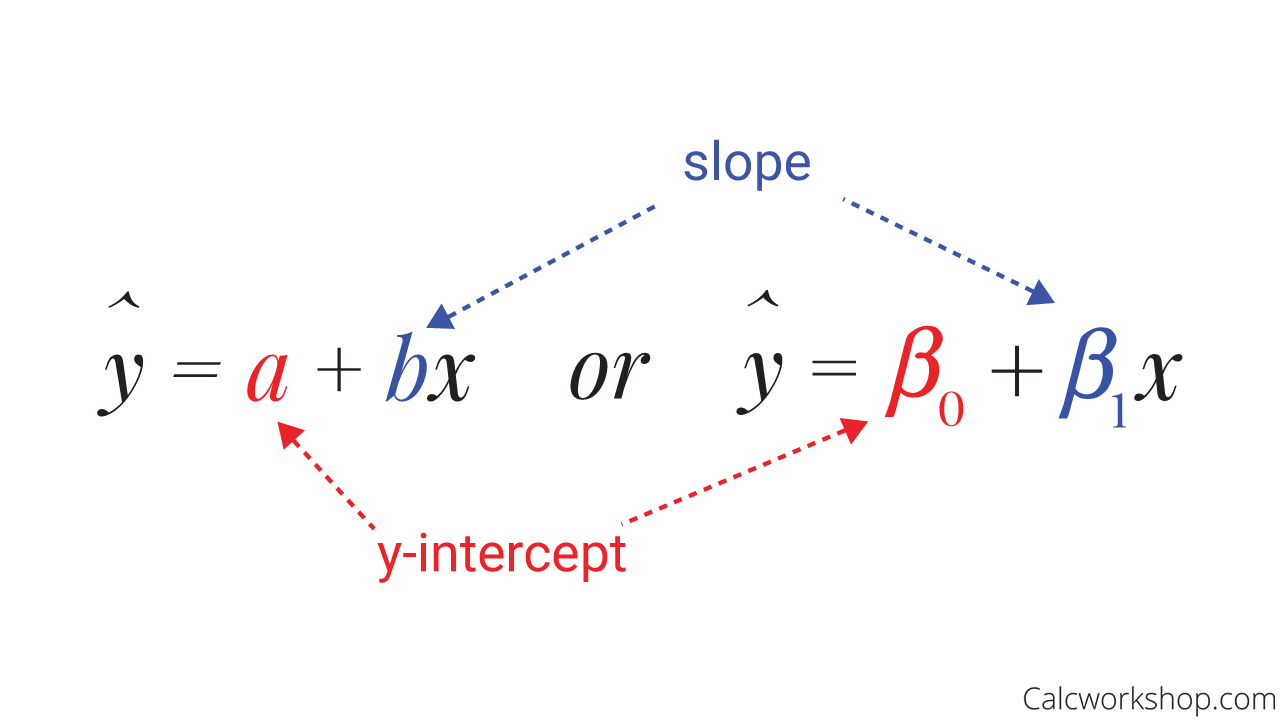
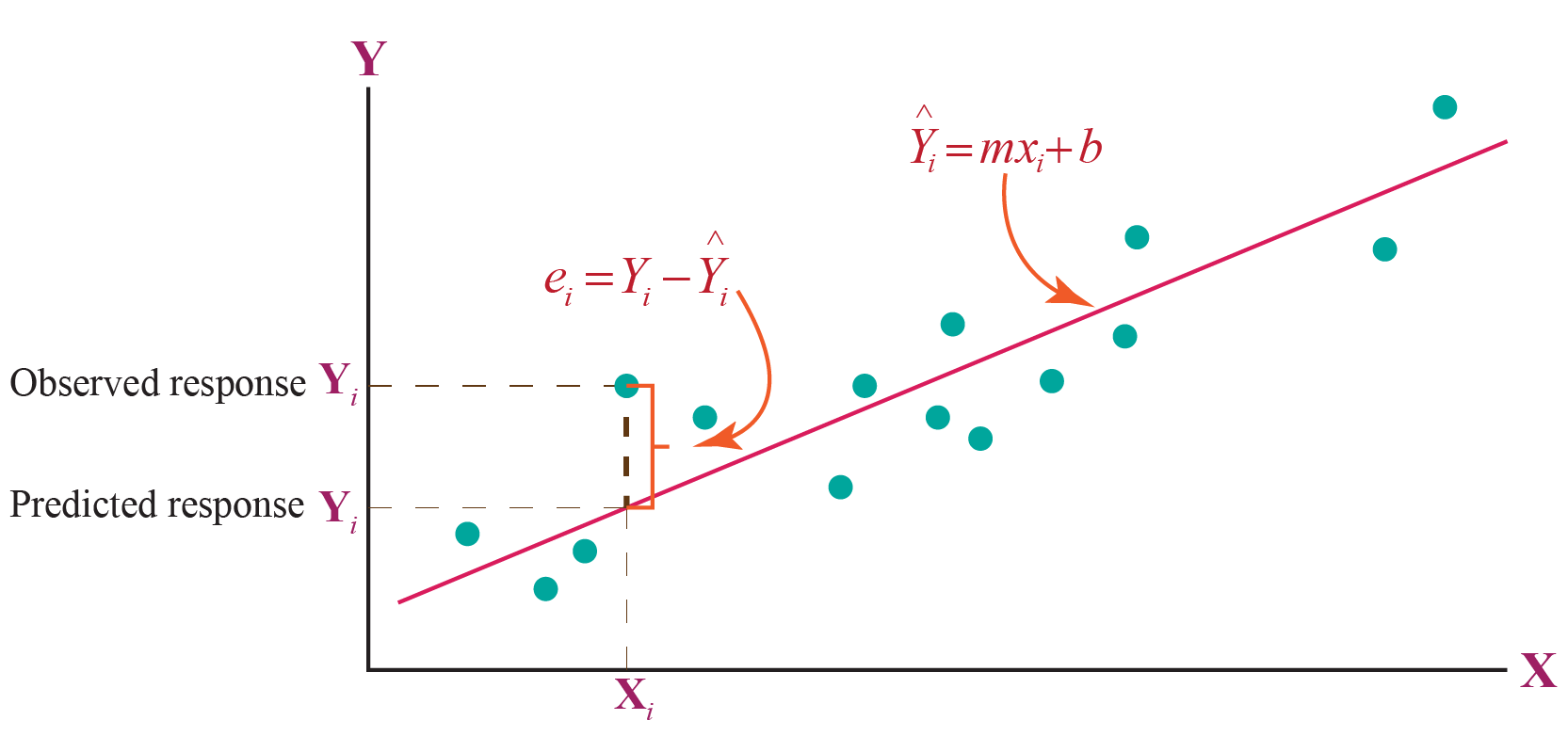
Least Squares Regression Line W 19 Worked Examples In linear regression, a residual is the difference between the actual value and the value predicted by the model (y ŷ) for any given point. a least squares regression model minimizes the sum of the squared residuals. Least squares is a method to apply linear regression. it helps us predict results based on an existing set of data as well as clear anomalies in our data. anomalies are values that are too good, or bad, to be true or that represent rare cases.
Least Squares Cuemath

Comments are closed.