The Fibonacci Sequence All About Fibonacci
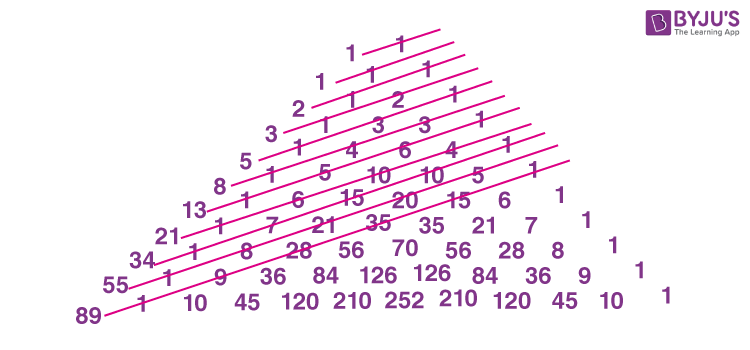
Fibonacci Numbers Definition Fibonacci Sequence Formula And Examples Fibonacci sequence. in mathematics, the fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. numbers that are part of the fibonacci sequence are known as fibonacci numbers, commonly denoted fn . many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 [1][2] and some (as. Fibonacci was not the first to know about the sequence, it was known in india hundreds of years before! about fibonacci the man. his real name was leonardo pisano bogollo, and he lived between 1170 and 1250 in italy. "fibonacci" was his nickname, which roughly means "son of bonacci".
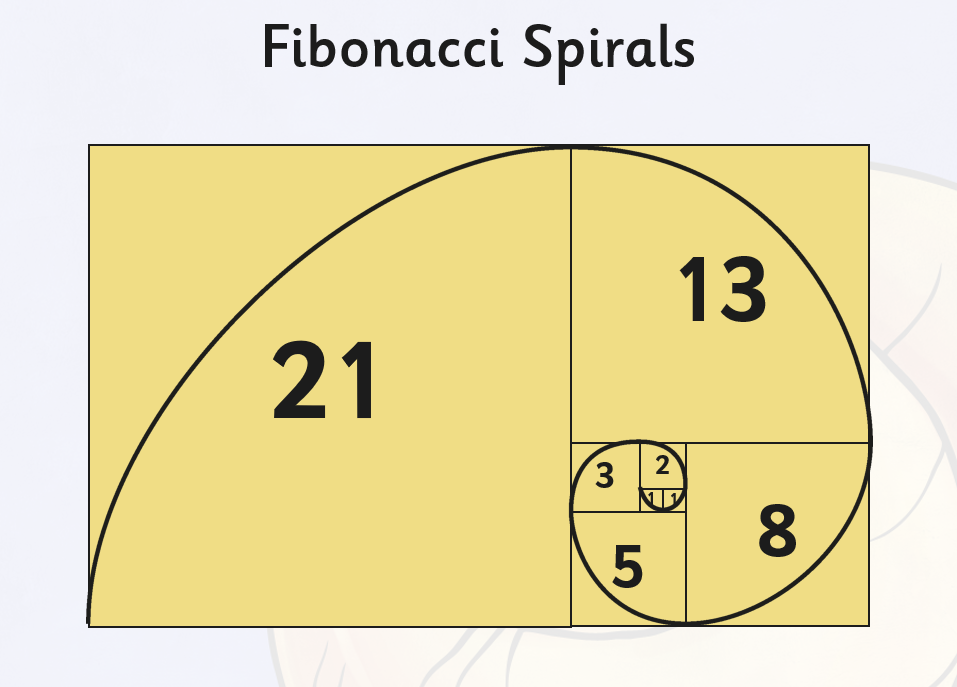
What Is The Fibonacci Sequence Answered Twinkl Teaching Wiki The numbers in the fibonacci sequence are also called fibonacci numbers. in maths, the sequence is defined as an ordered list of numbers that follow a specific pattern. the numbers present in the sequence are called the terms. the different types of sequences are arithmetic sequence, geometric sequence, harmonic sequence and fibonacci sequence. Fibonacci sequence, the sequence of numbers 1, 1, 2, 3, 5, 8, 13, 21, …, each of which, after the second, is the sum of the two previous numbers. the numbers of the sequence occur throughout nature, and the ratios between successive terms of the sequence tend to the golden ratio. Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034.
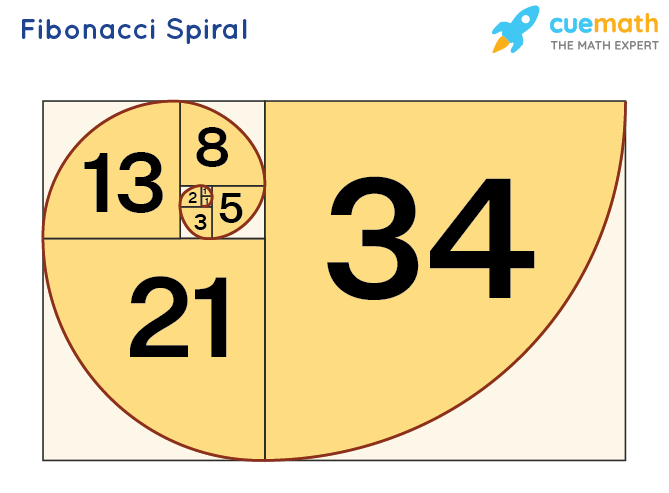
Fibonacci Sequence Formula Spiral Properties Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034. The fibonacci sequence is an integer sequence defined by a simple linear recurrence relation. the sequence appears in many settings in mathematics and in other sciences. in particular, the shape of many naturally occurring biological organisms is governed by the fibonacci sequence and its close relative, the golden ratio. the first few terms are. The fibonacci sequence. every number in the sequence is generated by adding together the two previous numbers. so the next fibonacci number is 13 21 = 34. they are the simplest example of a recursive sequence where each number is generated by an equation in the previous numbers in the sequence. hidden inside this sequence is another important.

Fibonacci Sequence Definition Formula List And Examples The fibonacci sequence is an integer sequence defined by a simple linear recurrence relation. the sequence appears in many settings in mathematics and in other sciences. in particular, the shape of many naturally occurring biological organisms is governed by the fibonacci sequence and its close relative, the golden ratio. the first few terms are. The fibonacci sequence. every number in the sequence is generated by adding together the two previous numbers. so the next fibonacci number is 13 21 = 34. they are the simplest example of a recursive sequence where each number is generated by an equation in the previous numbers in the sequence. hidden inside this sequence is another important.
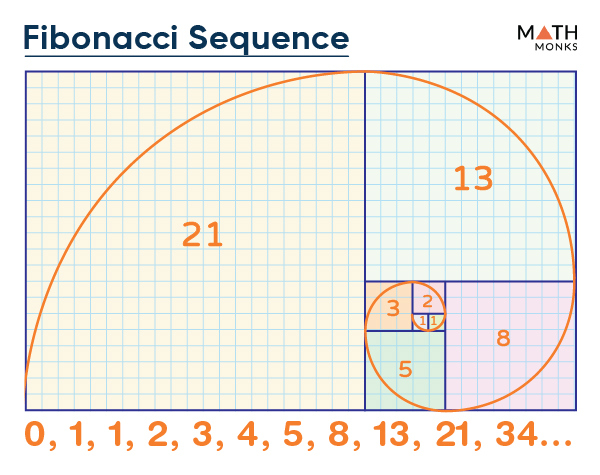
Fibonacci Sequence Definition Formula List Examples Diagrams

Comments are closed.