The Equation Of The Tangents To The Circle X2 Y2 25 And Making Intercepts
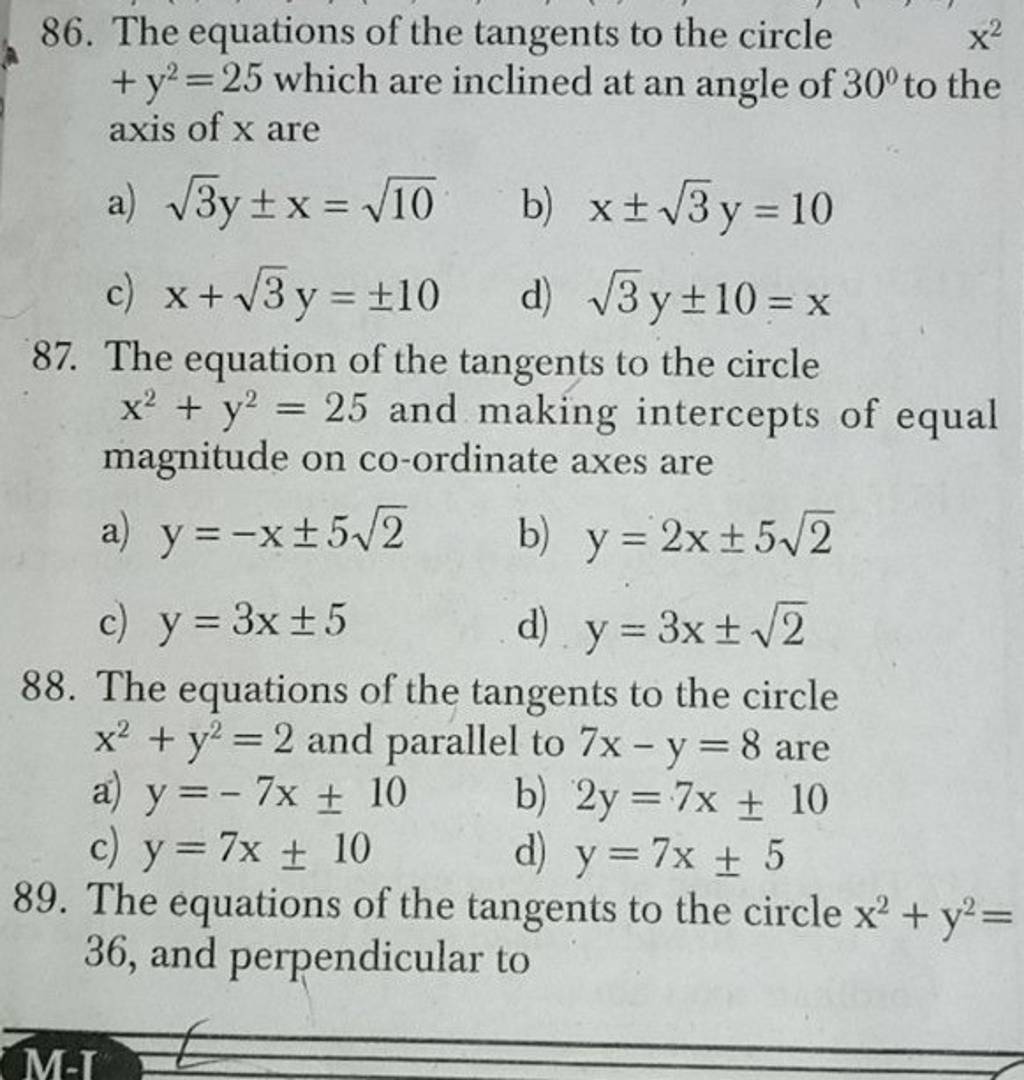
The Equation Of The Tangents To The Circle X2 Y2 25 And Making Intercepts Free tangent line calculator find the equation of the tangent line given a point or the intercept step by step. A tangent to a circle is a line which intersects the circle in exactly one point. in figure 1 line ab←→ a b ↔ is a tangent, intersecting circle o o just at point p p. figure 1. ab←→ a b ↔ is tangent to circle o o at point p p. a tangent has the following important property: theorem 7.3.1 7.3. 1. a tangent is perpendicular to the.
The Equation Of The Tangents To The Circle X2 Y2 25 And Making Intercepts Use the point slope formula y k = m(x h) the point (h,k) = ( 2,2) and m=1, so the line is y 2=(1)(x 2) or y=x 4 the tangent line at that point is just the y=x diagonal line through the origin shifted up by 4 units. or if you're into calculus, calculate the slope by taking the first derivative of the circle equation, with implicit differentiation. Tangent is a line and to write the equation of a line we need two things: 1. slope (m) 2. a point on the line. general equation of the tangent to a circle: 1) the tangent to a circle equation x 2 y 2 = a 2 for a line y = mx c is given by the equation y = mx ± a √ [1 m 2]. 2) the tangent to a circle equation x 2 y 2 = a 2 at (a1,b1) a 1. Y = 3 4x 25 4 we could use calculus but first as with all mathematical problems one should step back and think about what the question is asking you, and in this case we can easily answer the question using knowledge of the equation, in this case: x^2 y^2 = 25 represents a circle of centre (a,b)=(0,0) and radius r=5 first verify that (3, 4) actually lies on the circle; subs x=3 oito the. I am given the equation of a circle: $(x 2)^2 (y 7)^2 = 25$. the radius is $5$. center of the circle: $( 2, 7)$. two lines tangent to this circle pass through point $(4, 3)$, which is outside of said circle. how would i go about finding one of the equations of the lines tangent to the circle?.
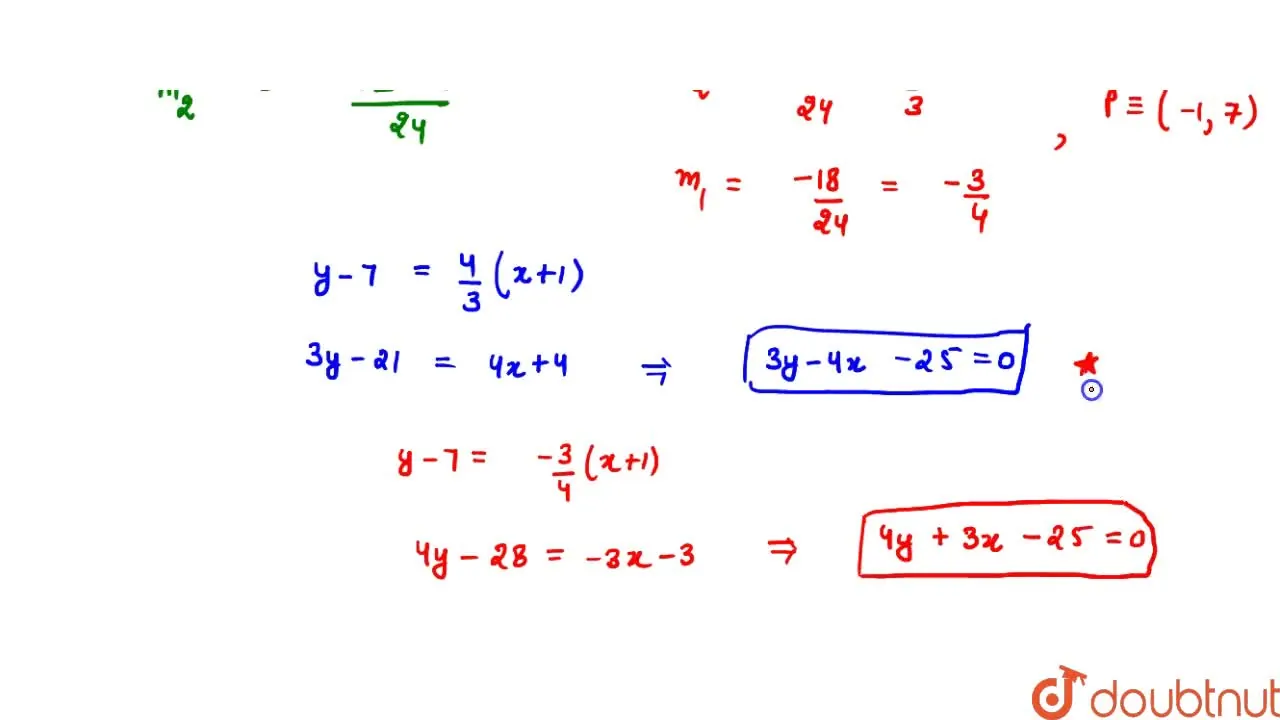
Find The Equations Of Tangents To The Circle X 2 Y 2 25 Which Pass Y = 3 4x 25 4 we could use calculus but first as with all mathematical problems one should step back and think about what the question is asking you, and in this case we can easily answer the question using knowledge of the equation, in this case: x^2 y^2 = 25 represents a circle of centre (a,b)=(0,0) and radius r=5 first verify that (3, 4) actually lies on the circle; subs x=3 oito the. I am given the equation of a circle: $(x 2)^2 (y 7)^2 = 25$. the radius is $5$. center of the circle: $( 2, 7)$. two lines tangent to this circle pass through point $(4, 3)$, which is outside of said circle. how would i go about finding one of the equations of the lines tangent to the circle?. Graph x^2 y^2=25. x2 y2 = 25 x 2 y 2 = 25. this is the form of a circle. use this form to determine the center and radius of the circle. (x−h)2 (y−k)2 = r2 (x h) 2 (y k) 2 = r 2. match the values in this circle to those of the standard form. the variable r r represents the radius of the circle, h h represents the x offset from. Question: find the equations of the lines tangent to the circle x2 y2=25 at the points where x= 4 in the xy plane. where do these (four) lines intersect and what is the shape and the area of the resulting quadrilateral? illustrate your results with a sketch of the circle and the tangents.
Solution Find The Equation Of The Line Tangent To The Circle X2 Y2 Graph x^2 y^2=25. x2 y2 = 25 x 2 y 2 = 25. this is the form of a circle. use this form to determine the center and radius of the circle. (x−h)2 (y−k)2 = r2 (x h) 2 (y k) 2 = r 2. match the values in this circle to those of the standard form. the variable r r represents the radius of the circle, h h represents the x offset from. Question: find the equations of the lines tangent to the circle x2 y2=25 at the points where x= 4 in the xy plane. where do these (four) lines intersect and what is the shape and the area of the resulting quadrilateral? illustrate your results with a sketch of the circle and the tangents.
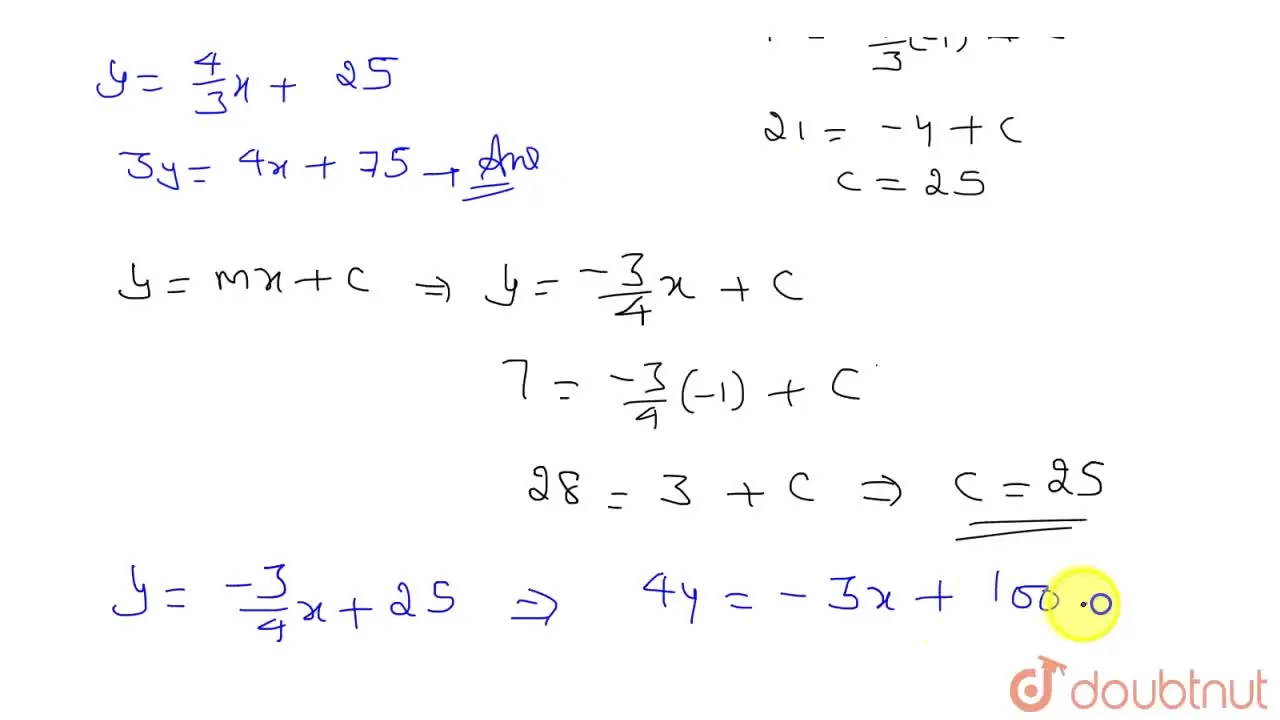
Find The Equations Of Tangents To The Circle X 2 Y 2 25 Which Pass

Comments are closed.