Teorema Fundamental Del Calculo Integral Bien Explicado Teorema
Teorema Fundamental Del Cálculo Integral Bien Explicado Teorema Teorema fundamental del cálculo, parte 1: integrales y antiderivadas. como se dijo anteriormente, el teorema fundamental del cálculo es un teorema extremadamente poderoso que establece la relación entre la diferenciación y la integración, y nos da una manera de evaluar integrales definidas sin usar sumas de riemann o calcular áreas. Este es uno de los puntos más importantes dentro del teorema fundamental del cálculo integral, porque esto significa que es doblemente importante. porque es un método para calcular integrales definidas con tener solo la función f' (x) = f (x). luego se deja calcular aplicando los límites de integración, de modo que pueda representar un.
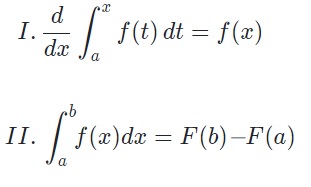
Teorema Fundamental Del Cálculo Integral Bien Explicado Teorema El teorema fundamental del cálculo, parte 1 muestra la relación entre la derivada y la integral. el teorema fundamental del cálculo, parte 2 es una fórmula para evaluar una integral definida en términos de una antiderivada de su integrando. el área total bajo una curva se puede encontrar usando esta fórmula. Este video fue financiado como proyecto novus. iniciativa del tecnológico de monterrey.en este video te explico de dónde viene, qué es, para qué sirve y cómo. Como f(t) = t 2 1 es una función continua, para calcular f ' (x) aplicamos el teorema fundamental del cálculo integral: 2) calcular la derivada de la siguiente función: puesto que f(t) es una función continua en el intervalo (0, ∞) aplicando el teorema fundamental del cálculo tenemos que:. En otras palabras: por definición, ya que es el área bajo la curva sobre el intervalo de longitud cero. por lo tanto, y así. lo que prueba la parte ii del teorema. 3. nota: en algunos libros de texto la parte i se llama el primer teorema fundamental del cálculo y la parte ii se llama el segundo teorema fundamental del cálculo.

Primer Teorema Fundamental Del Cálculo Profe Fily Como f(t) = t 2 1 es una función continua, para calcular f ' (x) aplicamos el teorema fundamental del cálculo integral: 2) calcular la derivada de la siguiente función: puesto que f(t) es una función continua en el intervalo (0, ∞) aplicando el teorema fundamental del cálculo tenemos que:. En otras palabras: por definición, ya que es el área bajo la curva sobre el intervalo de longitud cero. por lo tanto, y así. lo que prueba la parte ii del teorema. 3. nota: en algunos libros de texto la parte i se llama el primer teorema fundamental del cálculo y la parte ii se llama el segundo teorema fundamental del cálculo. F' (x)=f (x) para todo x en [a, b], entonces: es uno de los puntos más importantes dentro del teorema fundamental del cálculo integral, debido a que esto quiere decir que tiene una importancia doble. debido a que es un método para calcular integrales definidas con solo obtener la función f' (x)=f (x). está luego permite que se pueda. 5.4: el teorema fundamental del cálculo. dejar f(t) ser una función continua definida en [a, b]. la integral definitiva ∫b af(x)dx es el “área bajo f ” en [a, b]. podemos convertir este concepto en una función dejando variar el límite superior (o inferior). vamos f(x) = ∫x af(t)dt.
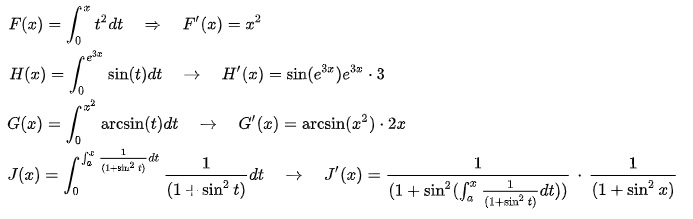
Teorema Fundamental Del Cálculo Integral Bien Explicado Teorema F' (x)=f (x) para todo x en [a, b], entonces: es uno de los puntos más importantes dentro del teorema fundamental del cálculo integral, debido a que esto quiere decir que tiene una importancia doble. debido a que es un método para calcular integrales definidas con solo obtener la función f' (x)=f (x). está luego permite que se pueda. 5.4: el teorema fundamental del cálculo. dejar f(t) ser una función continua definida en [a, b]. la integral definitiva ∫b af(x)dx es el “área bajo f ” en [a, b]. podemos convertir este concepto en una función dejando variar el límite superior (o inferior). vamos f(x) = ∫x af(t)dt.

El Teorema Fundamental Del Cálculo Demostración Curso De Cálculo

Comments are closed.