Techniques To Solve A System Of Equations Solved Examples

Techniques To Solve A System Of Equations Solved Examples Example 4.6.3. write each system of linear equations as an augmented matrix: ⓐ {11x = − 9y − 5 7x 5y = − 1 ⓑ {5x − 3y 2z = − 5 2x − y − z = 4 3x − 2y 2z = − 7. it is important as we solve systems of equations using matrices to be able to go back and forth between the system and the matrix. the next example asks us to. System of equations. solve the system of equations. distribute, then solve by elimination. add, and solve for j. substitute j = 347 into one of the original equations, then solve for w. check the answer in the problem. with the tailwind, the actual rate of the jet would be 347 18 = 365 mph. in 3 hours the jet would travel.

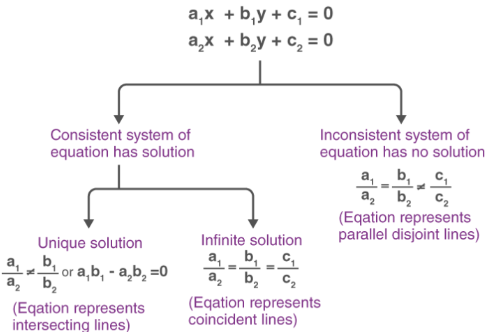
Solving System Of Equations With 3 Variables Solve the system by substitution. {− x y = 4 4x − y = 2. answer. in example 5.2.7 it was easiest to solve for y in the first equation because it had a coefficient of 1. in example 5.2.10 it will be easier to solve for x. Introduction to system of equations. a system of equations is a set or collection of equations that are dealt together. these equations can be solved graphically and algebraically. the point where two lines intersect is the solution to the system of equations. this article elaborates on the algebraic technique to solve system of equations. There are three ways to solve systems of linear equations: substitution, elimination, and graphing. let’s review the steps for each method. substitution. get a variable by itself in one of the equations. take the expression you got for the variable in step 1, and plug it (substitute it using parentheses) into the other equation. solve the. Example: solve these two equations: x y = 6; −3x y = 2; the two equations are shown on this graph: our task is to find where the two lines cross. well, we can see where they cross, so it is already solved graphically. but now let's solve it using algebra! hmmm how to solve this? there can be many ways!.
Techniques To Solve A System Of Equations Solved Examples There are three ways to solve systems of linear equations: substitution, elimination, and graphing. let’s review the steps for each method. substitution. get a variable by itself in one of the equations. take the expression you got for the variable in step 1, and plug it (substitute it using parentheses) into the other equation. solve the. Example: solve these two equations: x y = 6; −3x y = 2; the two equations are shown on this graph: our task is to find where the two lines cross. well, we can see where they cross, so it is already solved graphically. but now let's solve it using algebra! hmmm how to solve this? there can be many ways!. You can substitute 11 in for xx and 55 in for yy into the equations to see that they are the solution. x y = 6 → 1 5 = 6 x y = 6 → 1 5 = 6 − 3x y = 2 → − 3(1) 5 = 2 −3x y = 2 → −3(1) 5 = 2 . when solving a system of linear equations there are three possible outcomes. step by step guide: solving systems of equations by. Summary. systems of equations in two variables are useful for solving a variety of application problems. they can find break even points in business applications, solve total value problems and mixture problems, and solve for unknowns in problems of motion. often a chart or table can be useful to organize information that is known or unknown.

Math Example Systems Of Equations Solving Linear Systems By You can substitute 11 in for xx and 55 in for yy into the equations to see that they are the solution. x y = 6 → 1 5 = 6 x y = 6 → 1 5 = 6 − 3x y = 2 → − 3(1) 5 = 2 −3x y = 2 → −3(1) 5 = 2 . when solving a system of linear equations there are three possible outcomes. step by step guide: solving systems of equations by. Summary. systems of equations in two variables are useful for solving a variety of application problems. they can find break even points in business applications, solve total value problems and mixture problems, and solve for unknowns in problems of motion. often a chart or table can be useful to organize information that is known or unknown.

Comments are closed.