Tangents To An Ellipse

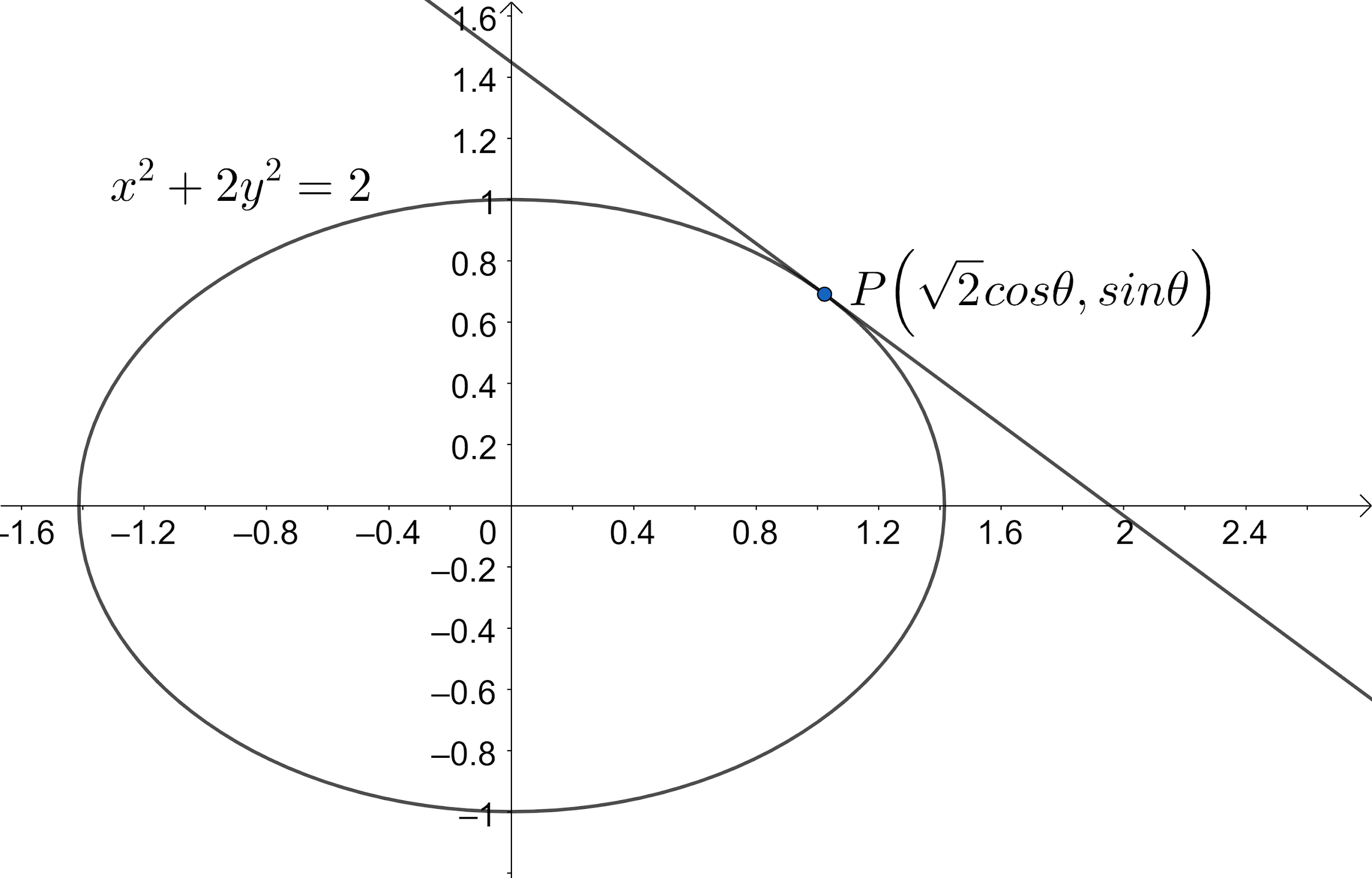
How To Find The Equation Of Tangents To An Ellipse At A Specific Point 593 The straight line y = mx ∓ √[a 2 m 2 b 2] represents the tangents to the ellipse. point form of a tangent to an ellipse; the equation of the tangent to an ellipse x 2 a 2 y 2 b 2 = 1 at the point (x 1, y 1) is xx 1 a 2 yy 1 b 2 = 1. the parametric form of a tangent to an ellipse; the equation of the tangent at any point (a. Tangent to an ellipse. try this drag any orange dot. note the tangent line touches at just one point. the blue line on the outside of the ellipse in the figure above is called the "tangent to the ellipse". another way of saying it is that it is "tangential" to the ellipse. (pronounced "tan gen shull"). it is a similar idea to the tangent to a.

Ellipse Line Equation Tangent Example Aesl The normal to an ellipse at a point p intersects the ellipse at another point q. the angle corresponding to q can be found by solving the equation (p q)· (dp) (dt)=0 (1) for t^', where p (t)= (acost,bsint) and q (t)= (acost^',bsint^'). this gives solutions t^'= cos^ ( 1) [ (n (t)) (a^4sin^2t b^4cos^2t)], (2) where (3) of which. The equation y = mx ± √[a 2 m 2 b 2] represents the tangents to the ellipse. point form of a tangent to an ellipse: the equation of the tangent to an ellipse given by x 2 a 2 y 2 b 2 = 1 at a point (x 1, y 1) is xx 1 a 2 yy 1 b 2 = 1. parametric form of a tangent to an ellipse: the equation of the tangent at any point specified in. Use parametric equation of tangent to ellipse xcosø a ysinø b =1 since this satisfies (4,6) put x and y as 4 and 6 and you get a trigonometric equation. square on both sides and put sin^2ø as 1 cos^2ø you get two values of cos ø. find corresponding values of sinø and substitute in the original equation of tangent! hope it helps. cheers!. The equation of the tangent line to an ellipse x 2 a 2 y 2 b 2 = 1 with slope m is y = m x b 2 y 0. so far, it seems we need to know the y coordinate of the point of tangency to determine the equation of the line, which contradicts statement (2) above. this is where i spent quite some time finding the relationship of y0 with the slope.

Tangents To An Ellipse From A Point On And Off The Curve Youtube Use parametric equation of tangent to ellipse xcosø a ysinø b =1 since this satisfies (4,6) put x and y as 4 and 6 and you get a trigonometric equation. square on both sides and put sin^2ø as 1 cos^2ø you get two values of cos ø. find corresponding values of sinø and substitute in the original equation of tangent! hope it helps. cheers!. The equation of the tangent line to an ellipse x 2 a 2 y 2 b 2 = 1 with slope m is y = m x b 2 y 0. so far, it seems we need to know the y coordinate of the point of tangency to determine the equation of the line, which contradicts statement (2) above. this is where i spent quite some time finding the relationship of y0 with the slope. A tangent to a hyperbola is a line that has a single common point with the hyperbola and is not parallel to the asymptotes of the hyperbola. the equation of a hyperbola centered at the origin with the transverse axis along the x axis and conjugate axis along the y axis is given by. the equation of a tangent at a point m0(x0, y0) of the. θ) is. ax sec θ– by csc θ =a2–b2 a x sec. ⁡. θ – b y csc. ⁡. θ = a 2 – b 2. the locus of middle points of parallel chords of an ellipse is the diameter of the ellipse and has the equation. y = 2a m y = 2 a m. the condition for y = mx c y = m x c to be the tangent to the ellipse is.

How To Find The Equation Of Tangents To An Ellipse At A Specific Point A tangent to a hyperbola is a line that has a single common point with the hyperbola and is not parallel to the asymptotes of the hyperbola. the equation of a hyperbola centered at the origin with the transverse axis along the x axis and conjugate axis along the y axis is given by. the equation of a tangent at a point m0(x0, y0) of the. θ) is. ax sec θ– by csc θ =a2–b2 a x sec. ⁡. θ – b y csc. ⁡. θ = a 2 – b 2. the locus of middle points of parallel chords of an ellipse is the diameter of the ellipse and has the equation. y = 2a m y = 2 a m. the condition for y = mx c y = m x c to be the tangent to the ellipse is.