Tangent Line To A Circle Properties Easily Explained Understanding Circles Better

Tangent Line To A Circle Properties Easily Explained Understanding Tangent line to a circle properties easily explained is a lesson that will teach you the properties that occur when a tangent line intersects with a line. Tangent of a circle: definition. tangent in geometry is defined as a line that touches the circle at only one point. the point of contact of the tangent with the circle is known as the point of tangency. here, the line pq is the tangent to the circle with center o. the line pq touches the circle at only one point, a. the point a is the point of.

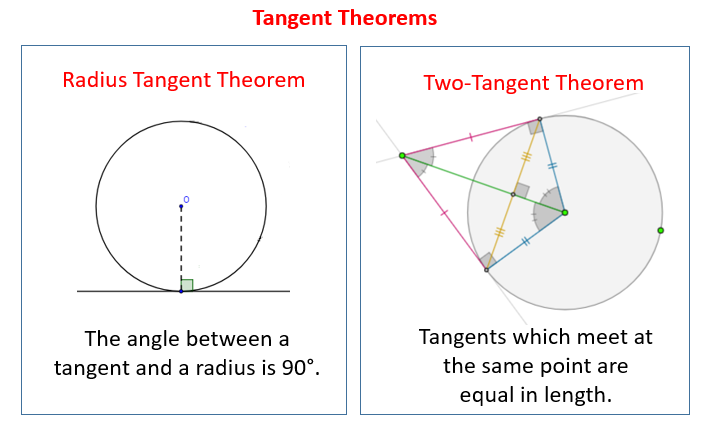
Tangents Of Circles Solutions Examples Videos A tangent to a circle is a line which intersects the circle in exactly one point. in figure 1 line ab←→ a b ↔ is a tangent, intersecting circle o o just at point p p. figure 1. ab←→ a b ↔ is tangent to circle o o at point p p. a tangent has the following important property: theorem 7.3.1 7.3. 1. a tangent is perpendicular to the. Tangent to a circle. a tangent to a circle is a straight line, in the plane of the circle, which touches the circle at only one point. the point is called the point of tangency or the point of contact. tangent to a circle theorem: a tangent to a circle is perpendicular to the radius drawn to the point of tangency. Knowing these essential theorems regarding circles and tangent lines, you are going to be able to identify key components of a circle, determine how many points of intersection, external tangents, and internal tangents two circles have, as well as find the value of segments given the radius and the tangent segment. video – lesson & examples. The sum of the measures of the interior angles of a quadrilateral is 360 ∘. this means that m∠paq m∠pcq = 360 ∘ − 90 ∘ − 90 ∘ = 180 ∘. therefore, ∠paq and ∠pcq are supplementary. in general, the angle between two lines tangent to a circle from the same point will be supplementary to the central angle created by the two.

Parts Of Circles Tangent Lines Ck 12 Foundation Knowing these essential theorems regarding circles and tangent lines, you are going to be able to identify key components of a circle, determine how many points of intersection, external tangents, and internal tangents two circles have, as well as find the value of segments given the radius and the tangent segment. video – lesson & examples. The sum of the measures of the interior angles of a quadrilateral is 360 ∘. this means that m∠paq m∠pcq = 360 ∘ − 90 ∘ − 90 ∘ = 180 ∘. therefore, ∠paq and ∠pcq are supplementary. in general, the angle between two lines tangent to a circle from the same point will be supplementary to the central angle created by the two. Line xy is tangent to circle at point . point is called the point of tangency. the radius drawn from the center of the circle to the point of tangency is always perpendicular to the tangent line. in the figure below, radius ‾ \overline {ax} is perpendicular to line . tangent lines of circles (kristakingmath) . Example 2: angles in the same segment. a, b, c, a, b,c, and d d are points on the circumference of a circle with center o. \, ac o.ac and bd b d intersect at point g. \, ef g.ef is a tangent at point c c and is parallel to bd. b d. calculate the size of angle bcf. bcf. locate the key parts of the circle for the theorem.

Tangent Circle Formula Learn The Formula Of Tangent Circle Along With Line xy is tangent to circle at point . point is called the point of tangency. the radius drawn from the center of the circle to the point of tangency is always perpendicular to the tangent line. in the figure below, radius ‾ \overline {ax} is perpendicular to line . tangent lines of circles (kristakingmath) . Example 2: angles in the same segment. a, b, c, a, b,c, and d d are points on the circumference of a circle with center o. \, ac o.ac and bd b d intersect at point g. \, ef g.ef is a tangent at point c c and is parallel to bd. b d. calculate the size of angle bcf. bcf. locate the key parts of the circle for the theorem.