Tangent Chord Angles Explanation And Examples Mastering Circles

Tangent Chord Angles Explanation And Examples Mastering Circles Tangent chord angles explanation and examples is a lesson that will teach you the properties that tangent chord angles have. the tangent chord angles are. An angle formed by a chord and a tangent that intersect on a circle is half the measure of the intercepted arc. $ x = \frac 1 2 \cdot \text{ m } \overparen{abc} $ note: like inscribed angles , when the vertex is on the circle itself, the angle formed is half the measure of the intercepted arc.

Tangent Chord Angles Theorem And Examples Youtube Find the degree measure for each angle or arc (problems #20 24) solve for x given intersecting chords, secants or tangents (problems #25 27) find the indicated angle, arc and segment length (problem #28) master circle geometry with our comprehensive guide, covering key concepts, theorems, and step by step examples for success. The chord tangent angle property states that the angle between a tangent and a chord at the point of contact is equal to the angle in the alternate segment. this property is useful in solving problems involving tangents and chords, especially when dealing with inscribed angles or proving relationships between angles in a circle. 5. Some tangent properties that you should keep in mind to help you solve problems include: 1) a tangent is perpendicular to the radius at the point of tangency. 2) tangent segments to an external point of a circle are equal. 3) the angle between a tangent and a chord is equal to the inscribed angle on the opposite side of that chord. Chords to tangents. the measure of an angle formed by a chord to a tangent is half the intercepted arc. arcs, semicircles, and central angles. central angle. a central angle c of a circle has its vertex at the center c of the circle. it separates the circle into two arcs: the minor arc and the major arc. chord and tangent intersection.
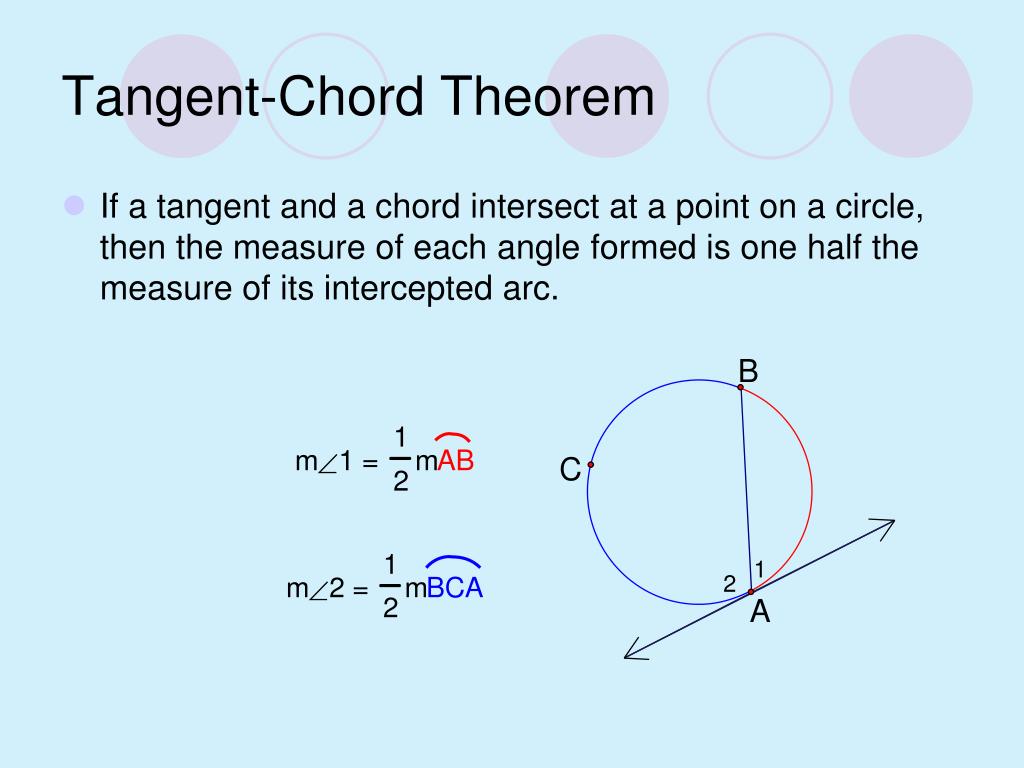
Ppt Circles Powerpoint Presentation Free Download Id 2409963 Some tangent properties that you should keep in mind to help you solve problems include: 1) a tangent is perpendicular to the radius at the point of tangency. 2) tangent segments to an external point of a circle are equal. 3) the angle between a tangent and a chord is equal to the inscribed angle on the opposite side of that chord. Chords to tangents. the measure of an angle formed by a chord to a tangent is half the intercepted arc. arcs, semicircles, and central angles. central angle. a central angle c of a circle has its vertex at the center c of the circle. it separates the circle into two arcs: the minor arc and the major arc. chord and tangent intersection. This theorem states that the angle formed between a chord and a tangent line to a circle is equal to the inscribed angle on the other side of the chord: ∠bad ≅ ∠bca. problem. prove the theorem. strategy. as we're dealing with a tangent line, we'll use the fact that the tangent is perpendicular to the radius at the point it touches the circle. A chord is a line segment whose endpoints lie on the circumference of a circle. a tangent is a line that touches a circle at exactly one point. this is called the point of tangency. an arc is a section of the circumference of a circle. a sector is a part of the interior of a circle, bounded by an arc and two radii.

Tangent Chord Angle Theorem This theorem states that the angle formed between a chord and a tangent line to a circle is equal to the inscribed angle on the other side of the chord: ∠bad ≅ ∠bca. problem. prove the theorem. strategy. as we're dealing with a tangent line, we'll use the fact that the tangent is perpendicular to the radius at the point it touches the circle. A chord is a line segment whose endpoints lie on the circumference of a circle. a tangent is a line that touches a circle at exactly one point. this is called the point of tangency. an arc is a section of the circumference of a circle. a sector is a part of the interior of a circle, bounded by an arc and two radii.

How To Find Central Angles Angles Involving Chords Tangents Of A

Comments are closed.