Taking Derivatives With Product Rule Calculus Mth101 Mathemagics

Taking Derivatives With Product Rule Calculus Mth101 Mathemagics Dive into the world of calculus with mehdi, your course lecturer at mathemagics! 📚 in this tutorial tailored for calculus 1: mth101, learn the ins and outs. Use product rule to find the instantaneous rate of change. so, all we did was rewrite the first function and multiply it by the derivative of the second and then add the product of the second function and the derivative of the first. and lastly, we found the derivative at the point x = 1 to be 86. now for the two previous examples, we had.

Product Rule For Derivative How To Take The Multiplication Derivative Summary of the product rule. the product rule is a very useful tool for deriving a product of at least two functions. it is a rule that states that the derivative of a product of two functions is equal to the first function f(x) in its original form multiplied by the derivative of the second function g(x) and then added to the original form of the second function g(x) multiplied by the. Use the product rule to compute the derivative of y = 5x2sinx. evaluate the derivative at x = π 2. solution. to make our use of the product rule explicit, let's set f(x) = 5x2 and g(x) = sinx. we easily compute recall that f′(x) = 10x and g′(x) = cosx. employing the rule, we have d dx(5x2sinx) = 5x2cosx 10xsinx. 3. derivatives. 3.1 the definition of the derivative; 3.2 interpretation of the derivative; 3.3 differentiation formulas; 3.4 product and quotient rule; 3.5 derivatives of trig functions; 3.6 derivatives of exponential and logarithm functions; 3.7 derivatives of inverse trig functions; 3.8 derivatives of hyperbolic functions; 3.9 chain rule. 1. remember when taking derivatives of the form (a x)b you need to take the derivative of what's inside as well. d(a x)b dx = b(a x)b−1d(a x) dx. so in your math, note that d(4−x)12 dx = 12(4 − x)11(−1) = −12(4 − x)11. once you take the individual derivatives of each function, use the product rule to put them all together. share.
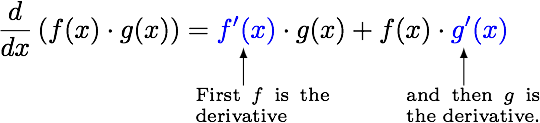
How To Use The Product Rule For Derivatives Visual Explanation With 3. derivatives. 3.1 the definition of the derivative; 3.2 interpretation of the derivative; 3.3 differentiation formulas; 3.4 product and quotient rule; 3.5 derivatives of trig functions; 3.6 derivatives of exponential and logarithm functions; 3.7 derivatives of inverse trig functions; 3.8 derivatives of hyperbolic functions; 3.9 chain rule. 1. remember when taking derivatives of the form (a x)b you need to take the derivative of what's inside as well. d(a x)b dx = b(a x)b−1d(a x) dx. so in your math, note that d(4−x)12 dx = 12(4 − x)11(−1) = −12(4 − x)11. once you take the individual derivatives of each function, use the product rule to put them all together. share. Quotient rule. d dx(f g) = f⋅g−f⋅g g2 d d x (f g) = f ′ ⋅ g − f ⋅ g ′ g 2. the numerator of the result resembles the product rule, but there is a minus instead of a plus; the minus sign goes with the g′ g ′. the denominator is simply the square of the original denominator – no derivatives there. example 2. Product rule. the product rule tells us the derivative of two functions f and g that are multiplied together: (the little mark ’ means "derivative of".) example: what is the derivative of cos (x)sin (x) ? we have two functions cos (x) and sin (x) multiplied together, so let's use the product rule: which in our case becomes: so we can substitute:.

Calculus Product Rule Video Lessons Examples Solutions Quotient rule. d dx(f g) = f⋅g−f⋅g g2 d d x (f g) = f ′ ⋅ g − f ⋅ g ′ g 2. the numerator of the result resembles the product rule, but there is a minus instead of a plus; the minus sign goes with the g′ g ′. the denominator is simply the square of the original denominator – no derivatives there. example 2. Product rule. the product rule tells us the derivative of two functions f and g that are multiplied together: (the little mark ’ means "derivative of".) example: what is the derivative of cos (x)sin (x) ? we have two functions cos (x) and sin (x) multiplied together, so let's use the product rule: which in our case becomes: so we can substitute:.

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog
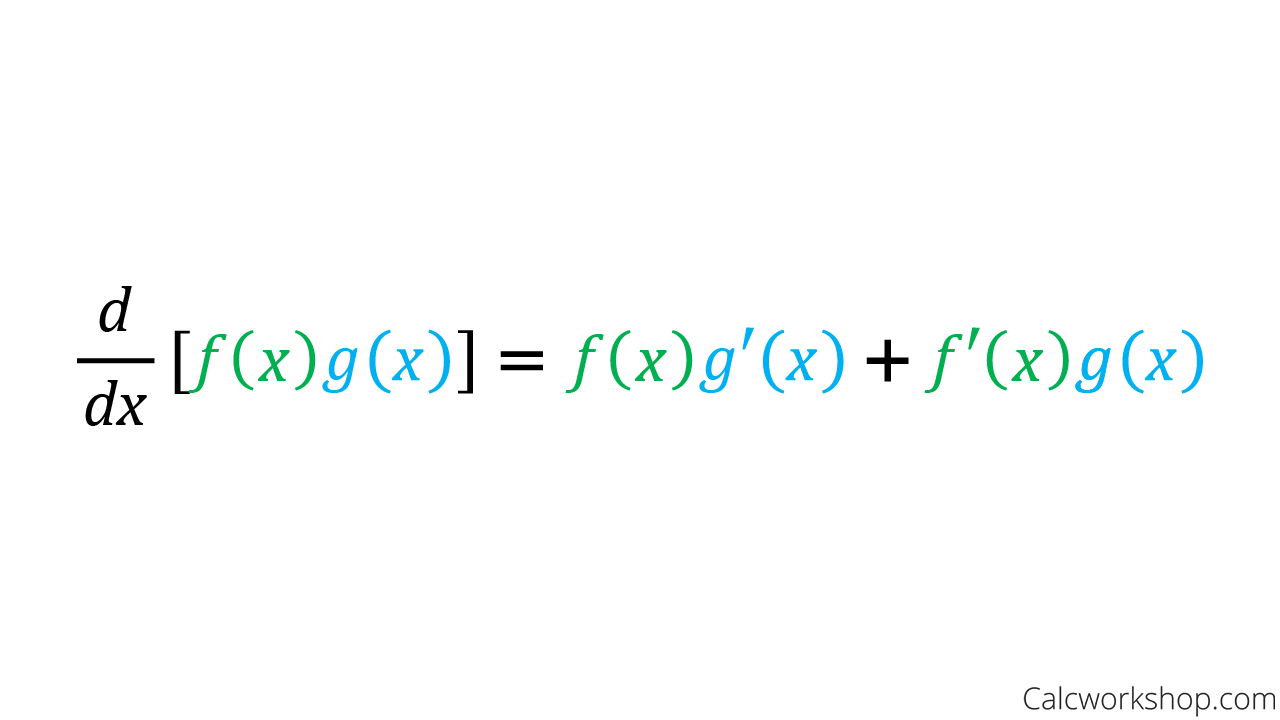
Product Rule For Calculus W Step By Step Examples

Comments are closed.