Sucesiones Aritmeticas Ejercicios Resueltos Y Para Resolver
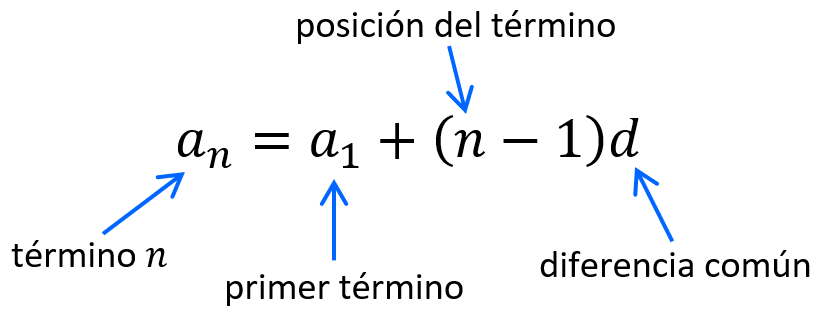
Sucesiones Aritméticas Ejercicios Resueltos Y Para Resolver Los ejercicios de sucesiones aritméticas pueden ser resueltos usando la fórmula de sucesiones aritméticas. esta fórmula nos permite encontrar cualquier número en la sucesión si es que conocemos la diferencia común, el primer término y la posición del número que queremos encontrar. a continuación, miraremos un resumen de sucesiones. Ahora que hemos visto algunos ejemplos resueltos, es momento de poner a prueba tus habilidades con ejercicios de sucesiones aritméticas. a continuación, presentamos una lista de ejercicios de sucesiones para que los resuelvas. 1. encuentra el 8º término en la sucesión con ( a 1 = 7 ) y ( d = 2 ). 2.

Ejercicios De Progresiones Aritméticas Practica Aritmética Y Problema 15. el primer término de una sucesión aritmética es a1 = 12 a 1 = 12 y la suma de los 5 primeros términos es s5 = 90 s 5 = 90 . calcular el término a5 a 5 y el término general a a n. resolvemos: la fórmula para calcular la suma es. como conocemos s5 = 90 s 5 = 90 y a1 =12 a 1 = 12, tenemos. En esta página repasamos los conceptos y fórmulas básicas de las sucesiones o progresiones aritméticas y resolvemos 15 15 problemas. Índice: progresión, términos y diferencia. monotonía (creciente o decreciente) término o fórmula general. suma de los primeros términos. 15 problemas resueltos. Ejercicio 1. encuentra el 10º término de la progresión aritmética cuyo primer término es 5 y cuya razón es 3. solución: identificamos los valores: a 1 = 5, d = 3, n = 10. sustituimos en la fórmula: a n = 5 (10 – 1) * 3. calculamos: a 10 = 5 27 = 32. por lo tanto, el 10º término es 32. Calcular la suma de los tres primeros términos de una sucesión geométrica de razón 0.5 sabiendo que su producto es 1000. soluciÓn. como la sucesión es geométrica y conocemos la razón, el término general es. an = a1 ⋅ 0.5n−1 a n = a 1 ⋅ 0.5 n − 1. sabemos que el producto de los tres primeros términos es 1000.

Sucesiones Numéricas Ejercicios Resueltos Psicotecnico Blog Del Ejercicio 1. encuentra el 10º término de la progresión aritmética cuyo primer término es 5 y cuya razón es 3. solución: identificamos los valores: a 1 = 5, d = 3, n = 10. sustituimos en la fórmula: a n = 5 (10 – 1) * 3. calculamos: a 10 = 5 27 = 32. por lo tanto, el 10º término es 32. Calcular la suma de los tres primeros términos de una sucesión geométrica de razón 0.5 sabiendo que su producto es 1000. soluciÓn. como la sucesión es geométrica y conocemos la razón, el término general es. an = a1 ⋅ 0.5n−1 a n = a 1 ⋅ 0.5 n − 1. sabemos que el producto de los tres primeros términos es 1000. 61 halla el primer término y la diferencia de una progresión aritmética, sabiendo que el quinto término es 47 y el décimo 97. solución: 10 5 a = a ( 10 − 5 )d ⇒ 97 = 47 5d ⇒ d = 10. a 5 = a 1 4 d ⇒ 47 = a 1 40 ⇒ a 1 = 7 solución: la suma de los ángulos de un cuadrilátero es s. Unidad 1 relaciones lógicas y conjuntos. unidad 2 sistema de los números naturales. unidad 3 sistema de los números enteros. unidad 4 sistema de los números racionales. unidad 5 sistema de los números reales. unidad 6 razones y proporciones. unidad 7 porcentajes. unidad 8 sucesiones y series.

Ejercicios De Sucesiones Aritmeticas Y Geometricas 61 halla el primer término y la diferencia de una progresión aritmética, sabiendo que el quinto término es 47 y el décimo 97. solución: 10 5 a = a ( 10 − 5 )d ⇒ 97 = 47 5d ⇒ d = 10. a 5 = a 1 4 d ⇒ 47 = a 1 40 ⇒ a 1 = 7 solución: la suma de los ángulos de un cuadrilátero es s. Unidad 1 relaciones lógicas y conjuntos. unidad 2 sistema de los números naturales. unidad 3 sistema de los números enteros. unidad 4 sistema de los números racionales. unidad 5 sistema de los números reales. unidad 6 razones y proporciones. unidad 7 porcentajes. unidad 8 sucesiones y series.

Comments are closed.