Substitution Method To Solve A System Of Equations
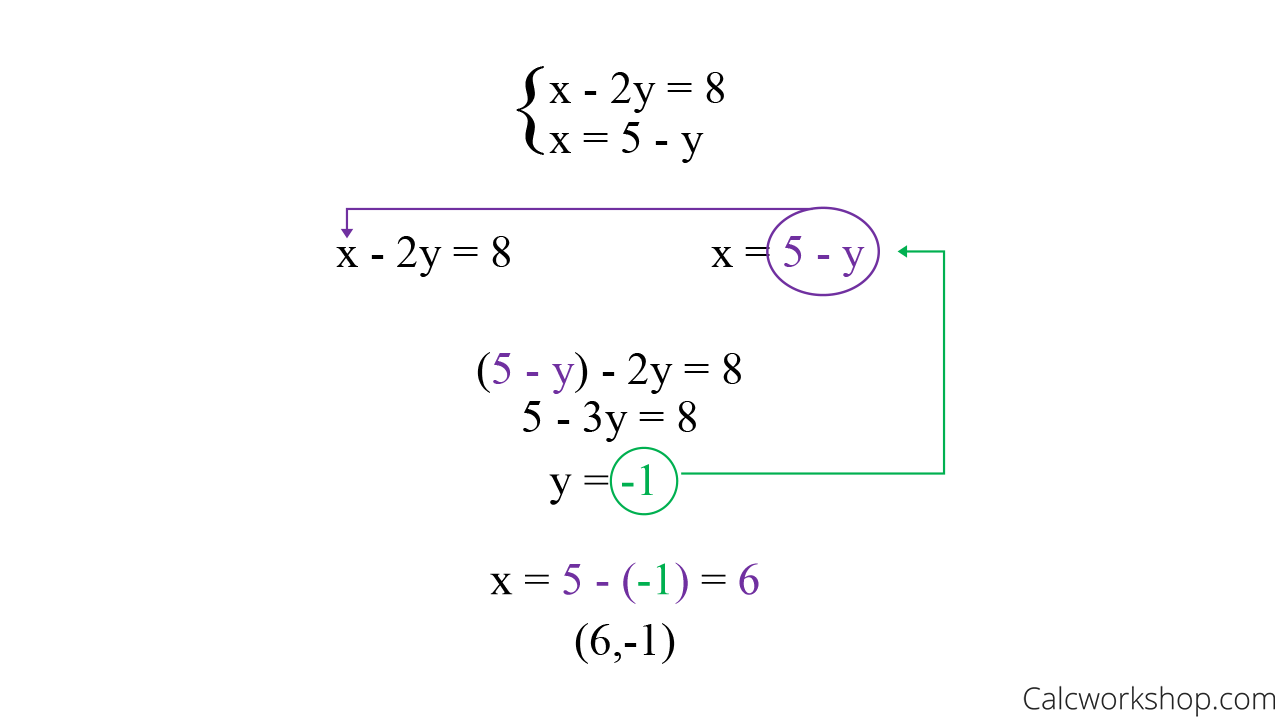
What Is The Substitution Method Just 3 Simple Steps Solve the system by substitution. {− x y = 4 4x − y = 2. answer. in example 5.2.7 it was easiest to solve for y in the first equation because it had a coefficient of 1. in example 5.2.10 it will be easier to solve for x. The substitution method is a technique for solving a system of equations. this article reviews the technique with multiple examples and some practice problems for you to try on your own.

Substitution Systems Of Equations The substitution method is a simple way to solve a system of linear equations algebraically and find the solutions of the variables. as the name suggests, it involves finding the value of the x variable in terms of the y variable from the first equation and then substituting or replacing the value of the x variable in the second equation. There are three ways to solve systems of linear equations: substitution, elimination, and graphing. let’s review the steps for each method. substitution. get a variable by itself in one of the equations. take the expression you got for the variable in step 1, and plug it (substitute it using parentheses) into the other equation. solve the. Whenever you arrive at a contradiction such as 3 = 4, your system of linear equations has no solutions. when you use these methods (substitution, graphing, or elimination) to find the solution what you're really asking is at what this system has no solutions. The substitution method. solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. we will consider two more algebraic methods of solving a system of linear equations that can always find an exact solution.

Ppt Solving Systems Of Equations The Substitution Method Powerpoint Whenever you arrive at a contradiction such as 3 = 4, your system of linear equations has no solutions. when you use these methods (substitution, graphing, or elimination) to find the solution what you're really asking is at what this system has no solutions. The substitution method. solving a linear system in two variables by graphing works well when the solution consists of integer values, but if our solution contains decimals or fractions, it is not the most precise method. we will consider two more algebraic methods of solving a system of linear equations that can always find an exact solution. So, the steps for using the substitution method to solve a system of linear equations are: rewrite one of the equations to isolate one variable. in the other equation, substitute the value of your isolated variable in for that variable. solve this second equation for the other variable. you should have a numerical value. Example 1: use the method of substitution to solve the system of linear equations below. the idea is to pick one of the two given equations and solve for either of the variables, . the result from our first step will be substituted into the other equation. the effect will be a single equation with one variable which can be solved as usual.

Substitution Method For Solving Systems Of Linear Equations 2 And 3 So, the steps for using the substitution method to solve a system of linear equations are: rewrite one of the equations to isolate one variable. in the other equation, substitute the value of your isolated variable in for that variable. solve this second equation for the other variable. you should have a numerical value. Example 1: use the method of substitution to solve the system of linear equations below. the idea is to pick one of the two given equations and solve for either of the variables, . the result from our first step will be substituted into the other equation. the effect will be a single equation with one variable which can be solved as usual.

Comments are closed.