Step Deviation Method Formula For Finding The Mean By Step Deviation

Step Deviation Method Formula For Finding The Mean By Step Deviation The step deviation method is also called a change of origin or scale method. what is the formula for step deviation method? to obtain the mean of large values, the formula of the step deviation method is applied. it is as follows: step deviation of mean = a h [∑u\( i\)f\( i\) ∑f\( i\)], where, a is the assumed mean; h is the class size. In the problems where the width of all classes is the same, then further simplify the calculations of the mean by computing the coded mean, i.e. the mean of u1, u2, u3, … un where, ui = (yi – a) c. then the mean is given by the formula, mean = a c x (Σfiui Σfi) this method of finding the mean is called the step deviation method.

Step Deviation Method Definition Formula Steps Examples Multiply the step deviations with the frequencies and take up the sum of the numbers so obtained. apply the formula: , where Σd1 is the sum of all the step deviations multiplied by respective frequencies and c represents the common factor. the number so obtained is the arithmetic mean of the given data set. thus, the formula for the. Find the mean of the following distribution using the step deviation method. solution: here, the intervals are of equal size. so we can apply the step deviation method, in which. a = a l ∙ ∑di′fi ∑fi ∑ d i ′ f i ∑ f i. where a = assumed mean, l = common size of class intervals. fi = frequency of the ith class interval. di. Mean by step deviation method. sometime during the application of short method (given above) of finding the a.m. if each deviation di d i are divisible by a common number h (let) let ui u i = di h d i h = xi–a h x i – a h, where a is assumed mean. ∴ ∴ x¯ x ¯ = a (∑fiui n ∑ f i u i n)h. example : find the a.m. of the following. Identify the class intervals and calculate the midpoint (x i) for each class. 3. choose an assumed mean (a): select one of the midpoints as the assumed mean (a). 4. calculate the step deviation (d i): compute the deviation of each midpoint from the assumed mean and then divide by the class width (h). this gives the step deviation: di=xi−ahd i.

Calculating The Mean Using Step Deviation Method Youtube Mean by step deviation method. sometime during the application of short method (given above) of finding the a.m. if each deviation di d i are divisible by a common number h (let) let ui u i = di h d i h = xi–a h x i – a h, where a is assumed mean. ∴ ∴ x¯ x ¯ = a (∑fiui n ∑ f i u i n)h. example : find the a.m. of the following. Identify the class intervals and calculate the midpoint (x i) for each class. 3. choose an assumed mean (a): select one of the midpoints as the assumed mean (a). 4. calculate the step deviation (d i): compute the deviation of each midpoint from the assumed mean and then divide by the class width (h). this gives the step deviation: di=xi−ahd i. Mean = sum of observations number of observations. depending on the size of the data, there are three ways to find the meaning of data collected, such as. direct method; assumed mean method; step deviation method; step deviation method. if the data values are large, a step deviation method is used to obtain the definition. the formula is. In this method, first, we need to choose the assumed mean, say “a” among the x i, which lies in the centre. (if we consider the same example, we can choose either a = 47.5 or 62.5). now, let us choose a = 47.5. the second step is to find the difference (d i) between each x i and the assumed mean “a”.

How To Find Mean Of Grouped Data By Step Deviation Method Youtube Mean = sum of observations number of observations. depending on the size of the data, there are three ways to find the meaning of data collected, such as. direct method; assumed mean method; step deviation method; step deviation method. if the data values are large, a step deviation method is used to obtain the definition. the formula is. In this method, first, we need to choose the assumed mean, say “a” among the x i, which lies in the centre. (if we consider the same example, we can choose either a = 47.5 or 62.5). now, let us choose a = 47.5. the second step is to find the difference (d i) between each x i and the assumed mean “a”.

Mean By Step Deviation Method Statistics Maths Class 10
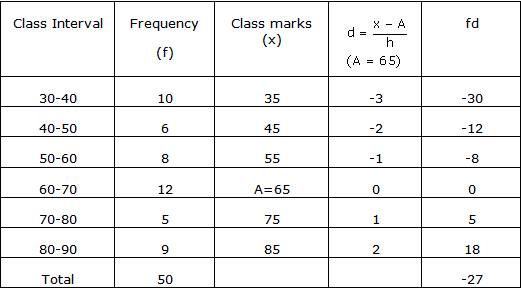
Using Step Deviation Method Find The Mean Of The Following Distribution

Comments are closed.