Solved Prove 1 3 2 3 N 3 1 2 N 2 I E Chegg

Solved Prove 1 3 2 3 N 3 1 2 N 2 I E Chegg We will prove this by mathematical induction. base case: when n=1, we have: (1) 2 = 1 3. view the full answer step 2. unlock. step 3. unlock. answer. Prove that 1^3 2^3 n^3 = (1 2 n)^2 for every positive integer n, using the principle of mathematical induction. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

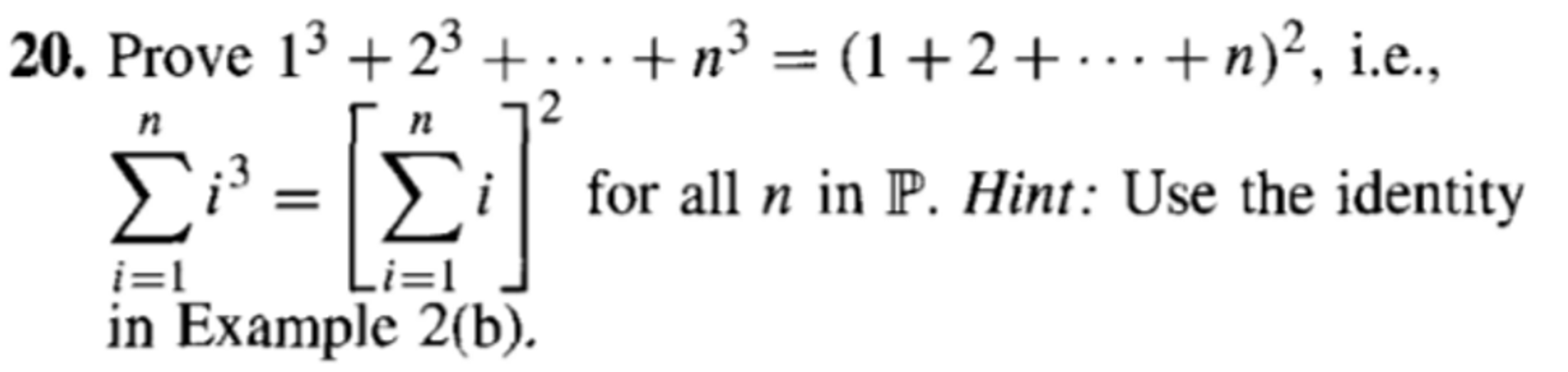
Solved Prove 1 3 2 3 N 3 1 2 N 2 I E Chegg Add a comment. 4. consider the case where n = 1. we have 13 = 12. now suppose 13 23 33 ⋯ n3 = (1 2 3 ⋯ n)2 for some n ∈ n. recall first that (1 2 3 ⋯ n) = n(n 1) 2 so we know 13 23 33 ⋯ n3 = (n(n 1) 2)2. Ex 4.1,2: prove the following by using the principle of mathematical induction 13 23 33 n3 = ( ( 1) 2)^2 let p (n) : 13 23 33 43 n3 = ( ( 1) 2)^2. Show each step in the following table. use mathematical induction to prove that: 1 3 2 3 3 3 n 3 = n 2 (n 1) 2 4 for all positive integers n. hint: the proof includes 3 steps. show each step in the following table. step 1: we first show that p (1) is true. step 2: we assume that p (k) is true. Question: problem 1 prove that 1 ·1! 2 ·2! 3 ·3! . n ·n! = (n 1)! −1 for all positive integers n ≥ 1 (not that ·represents the multiplication.

Prove That 1 3 2 3 3 3 N 3 N N 1 2 2 Teachoo Show each step in the following table. use mathematical induction to prove that: 1 3 2 3 3 3 n 3 = n 2 (n 1) 2 4 for all positive integers n. hint: the proof includes 3 steps. show each step in the following table. step 1: we first show that p (1) is true. step 2: we assume that p (k) is true. Question: problem 1 prove that 1 ·1! 2 ·2! 3 ·3! . n ·n! = (n 1)! −1 for all positive integers n ≥ 1 (not that ·represents the multiplication. I need to prove that $$ 2^n > n^3\quad \forall n\in \mathbb n, \;n>9.$$ now that is actually very easy if we prove it for real numbers using calculus. but i need a proof that uses mathematical induction. i tried the problem for a long time, but got stuck at one step i have to prove that: $$ k^3 > 3k^2 3k 1 $$ hints???. Answer to prove that 1^3 2^3 3^3 ? n^3=n^2 (n 1)^2 4. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved Problem 4 1 Prove That N N 1 2n 1 3n2 3n 1 Chegg I need to prove that $$ 2^n > n^3\quad \forall n\in \mathbb n, \;n>9.$$ now that is actually very easy if we prove it for real numbers using calculus. but i need a proof that uses mathematical induction. i tried the problem for a long time, but got stuck at one step i have to prove that: $$ k^3 > 3k^2 3k 1 $$ hints???. Answer to prove that 1^3 2^3 3^3 ? n^3=n^2 (n 1)^2 4. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

Solved Vi 1 1 2 1 2 3 1 2 3 N Chegg