Solved Differential Equations Solve The Initial Value Chegg

Solved Differential Equations Solve The Initial Value Chegg Differential equations solve the initial value problem y' y = 1 cost y(0) = 0 consider the differential equation t^(2)y'' 3ty' y = 0 t > 0 verify that y1(t) = t^( 1) is a solution. use the method of reduction of order to find a second solution to the differential equation. Answer to differential equations. solve the initial value. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.
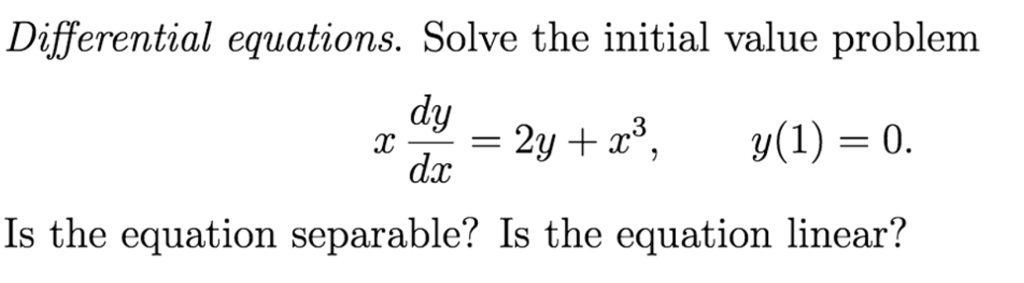
Solved Differential Equations Solve The Initial Value Chegg Question: differential equations solve the initial value problem this problem concerns the spring damper system we discussed in class (the primary example in chapter 14 of goodwine). recall that for free (that is, no forcing) damped vibration starting from rest at position x0, the position x(t) of the mass at time t satisfies the initial value. An ordinary differential equation (ode) is a mathematical equation involving a single independent variable and one or more derivatives, while a partial differential equation (pde) involves multiple independent variables and partial derivatives. odes describe the evolution of a system over time, while pdes describe the evolution of a system over. This is characteristic of the formal manipulative way in which the laplace transform is used to solve differential equations. any doubts about the validity of the method for solving a given equation can be resolved by verifying that the resulting function \(y\) is the solution of the given problem. 4.4 solving initial value problems having explored the laplace transform, its inverse, and its properties, we are now equipped to solve initial value problems (ivp) for linear differential equations. our focus will be on second order linear differential equations with constant coefficients.
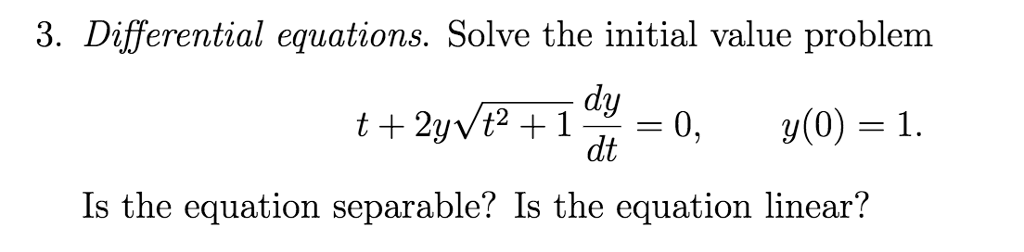
Solved Differential Equations Solve The Initial Value Chegg This is characteristic of the formal manipulative way in which the laplace transform is used to solve differential equations. any doubts about the validity of the method for solving a given equation can be resolved by verifying that the resulting function \(y\) is the solution of the given problem. 4.4 solving initial value problems having explored the laplace transform, its inverse, and its properties, we are now equipped to solve initial value problems (ivp) for linear differential equations. our focus will be on second order linear differential equations with constant coefficients. The final step, in which the particular solution is obtained using the initial or boundary values, involves mostly algebraic operations, and is similar for ivps and for bvps. ivps and bvps for linear differential equations are solved rather easily since the final algebraic step involves the solution of linear equations. A first order differential equation is an equation of the form f(t, y, ˙y) = 0. a solution of a first order differential equation is a function f(t) that makes f(t, f(t), f ′ (t)) = 0 for every value of t. here, f is a function of three variables which we label t, y, and ˙y. it is understood that ˙y will explicitly appear in the equation.

Solved Differential Equations Solve The Initial Value Chegg The final step, in which the particular solution is obtained using the initial or boundary values, involves mostly algebraic operations, and is similar for ivps and for bvps. ivps and bvps for linear differential equations are solved rather easily since the final algebraic step involves the solution of linear equations. A first order differential equation is an equation of the form f(t, y, ˙y) = 0. a solution of a first order differential equation is a function f(t) that makes f(t, f(t), f ′ (t)) = 0 for every value of t. here, f is a function of three variables which we label t, y, and ˙y. it is understood that ˙y will explicitly appear in the equation.

Comments are closed.