Solved An Undamped Spring Mass System Is Shown Below A Starting
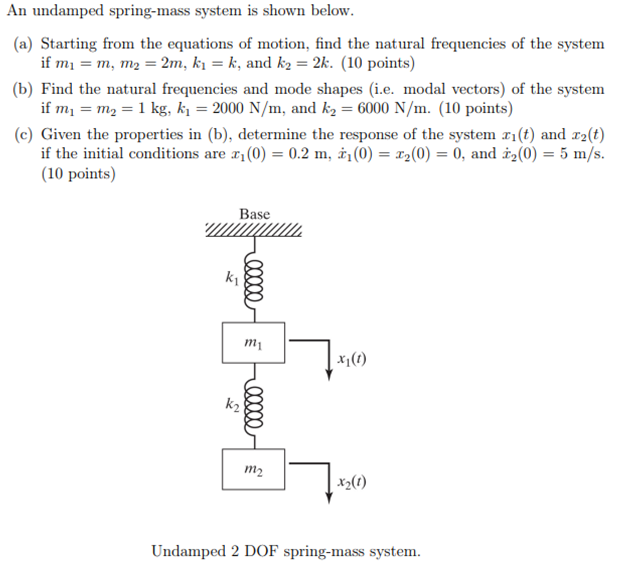
Solved An Undamped Spring Mass System Is Shown Below A Chegg An undamped spring mass system is shown below. (a) starting from the equations of motion, find the natural frequencies of the system if m 1 = m, m 2 = 2 m, k 1 = k, and k 2 = 2 k. (10 points) (b) find the natural frequencies and mode shapes (i.e. modal vectors) of the system if m 1 = m 2 = 1 kg, k 1 = 2000 n m, and k 2 = 6000 n m. An undamped spring mass system is shown below. a mass m = 1 kg moving with a velocity v 0 hits mass m = 10 kg at time t = 0 and gets embedded into it. what are the initial conditions to be used for the free vibration analysis of this system? x (0) = 0, x (0) = 10 v 0 x (0) = 0, x (0) = − 10 v 0 x (0) = 0, x (0) = − 11 v 0 x (0) = 0, x (0.
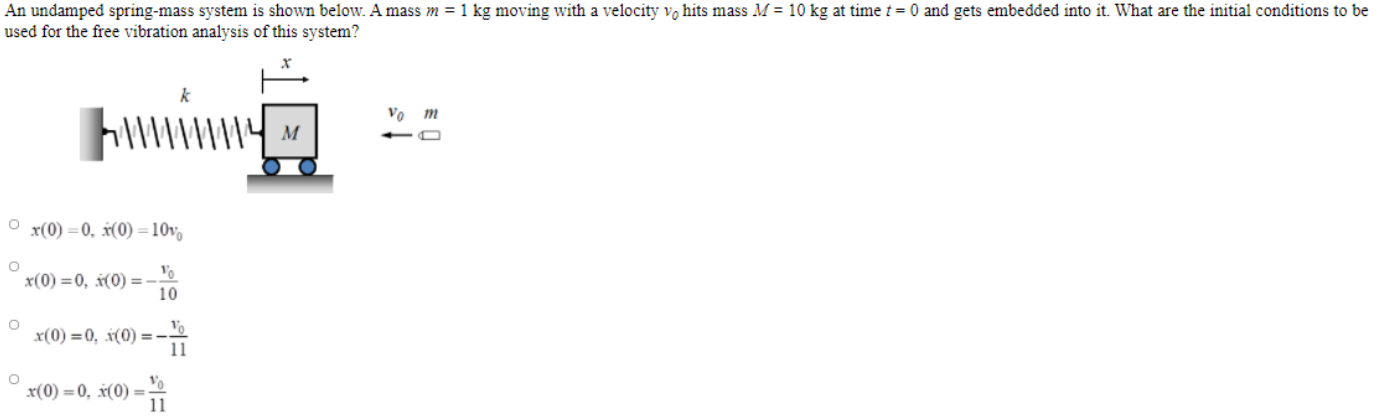
Solved An Undamped Spring Mass System Is Shown Below A Mass Chegg Spring mass system. next we appeal to newton’s law of motion: sum of forces = mass times acceleration to establish an ivp for the motion of the system; f = ma. there are two forces acting at the point where the mass is attached to the spring. the gravitational force, or weight of the mass m acts downward and has magnitude mg,. The angle ϕ in equation 6.1.10 is the phase angle. it’s measured in radians. equation 6.1.10 is the amplitude–phase form of the displacement. if t is in seconds then ω0 is in radians per second (rad s); it is the frequency of the motion. it is also called the natural frequency of the spring–mass system without damping. Undamped spring mass systems. m = kx dt2 − where k is the spring constant, m is the mass placed at the end of the spring and x(t) is the position of the mass at time t. example: a force of 400 newtons stretches a spring 2 meters. a mass of 50 kilograms is attached to the end of the spring and is initially released from the equilibrium. The basic vibration model of a simple oscillatory system consists of a mass, a massless spring, and a damper. if damping in moderate amounts has little influence on the natural frequency, it may be neglected. the system can then be considered to be conservative. an undamped spring mass system is the simplest free vibration system. it has one.
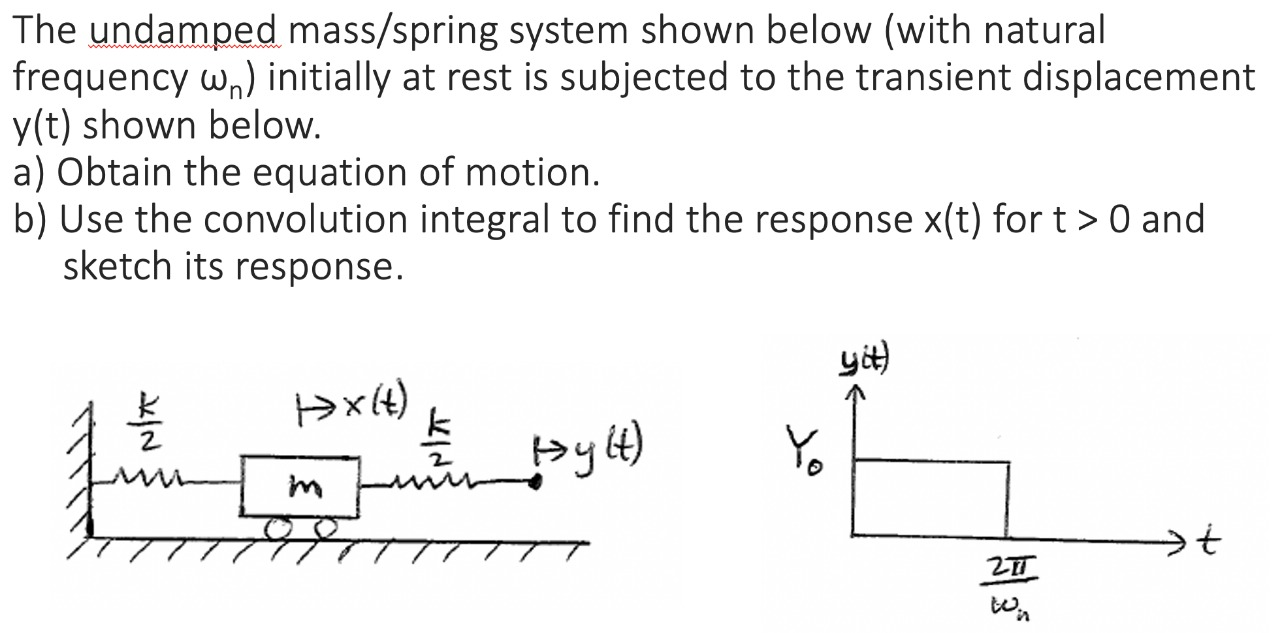
Solved The Undamped Mass Spring System Shown Below With Chegg Undamped spring mass systems. m = kx dt2 − where k is the spring constant, m is the mass placed at the end of the spring and x(t) is the position of the mass at time t. example: a force of 400 newtons stretches a spring 2 meters. a mass of 50 kilograms is attached to the end of the spring and is initially released from the equilibrium. The basic vibration model of a simple oscillatory system consists of a mass, a massless spring, and a damper. if damping in moderate amounts has little influence on the natural frequency, it may be neglected. the system can then be considered to be conservative. an undamped spring mass system is the simplest free vibration system. it has one. Transcribed image text: st 5. consider an undamped spring mass system m = 10 kg and k = 4000. this system is under a forced vibration f (t). use the "magnification factor" graph shown below: (1) what equation describes the relation between and ? (self exercise) determine x for: (2) f (t) = 400 sin (101) n. (5 pts) (3) f (t) = 800 cos (30t) n. A mass of 400 grams stretches a spring by 5 centimeters. (a) find the spring constant k, the angular frequency ω, as well as the period t and frequency f of free undamped motion for this spring mass system. (b) find the general solution of the de for the free spring mass system. (c) suppose that an exterior force of f(t) = 27sin(13t) newtons.

Solved A A Simple Undamped Spring Mass System As Shown In Chegg Transcribed image text: st 5. consider an undamped spring mass system m = 10 kg and k = 4000. this system is under a forced vibration f (t). use the "magnification factor" graph shown below: (1) what equation describes the relation between and ? (self exercise) determine x for: (2) f (t) = 400 sin (101) n. (5 pts) (3) f (t) = 800 cos (30t) n. A mass of 400 grams stretches a spring by 5 centimeters. (a) find the spring constant k, the angular frequency ω, as well as the period t and frequency f of free undamped motion for this spring mass system. (b) find the general solution of the de for the free spring mass system. (c) suppose that an exterior force of f(t) = 27sin(13t) newtons.

Comments are closed.