Solved 8 Challenge Prove The Following Theorem If Two Chegg

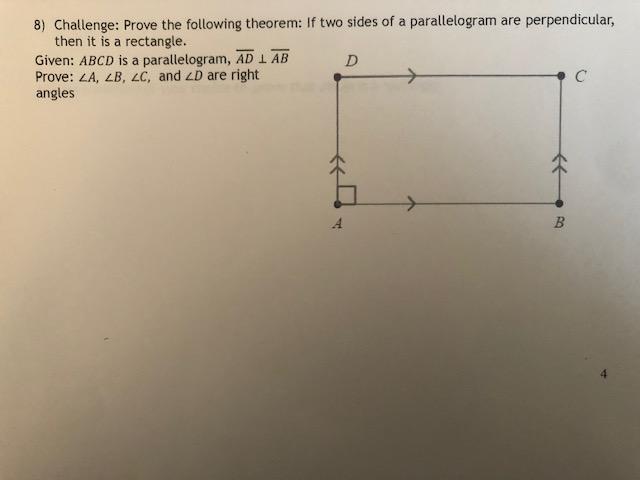
Solved 8 Challenge Prove The Following Theorem If Two Chegg Answer to solved 8) challenge: prove the following theorem: if two | chegg prove the following theorem: if two sides of a parallelogram are perpendicular. Solution. we know angle 1 = angle 3 (pair …. write a formal proof of the following theorem if two parallel lines are cut by a transversal, then the pairs of exterior angles on the same side of the transversal are supplementary 3 2 1 given: prove: select select statements reasons 1 select v 1 select select 2.

Solved Exercise 8 Prove The Following Theorem Theorem Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: prove the following theorem using a two column, statement reason format. given alp prove mz1 =m 2=m3= m 4 = 90° p reasons use a two column proot statements 1. q.lp 2 m21 3. m24mz1 = 4 m24 5.m24 1. 2.5.2apply the epsilon delta definition to find the limit of a function. 2.5.3describe the epsilon delta definitions of one sided limits and infinite limits. 2.5.4use the epsilon delta definition to prove the limit laws. by now you have progressed from the very informal definition of a limit in the introduction of this chapter to the intuitive. Ok, i'll show how i'd solve a: we have. f(x) = 1 x 2 − 1 x− −−−−√ f (x) = 1 x 2 − 1 x. clearly f(0) = 0 f (0) = 0. let's look at the derivative of f f. if we show that the derivative is strictly positive for x> 0 x> 0, the function is strictly increasing, hence positive (in combination with f(0) f (0)) for x> 0 x> 0. we. Theorem 8.6.1 leta be a realm×n matrix, and letσ1 ≥σ2 ≥···≥σr >0 be the positivesingular values ofa. thenr is the rank ofa and we have the factorization a=pΣaqt wherep andq are orthogonal matrices the factorization a =pΣaqt in theorem 8.6.1, where p and q are orthogonal matrices, is called a singular value decomposition (svd) of a.

Solved Question 8 Prove The Following Theorem Theorem For Chegg Ok, i'll show how i'd solve a: we have. f(x) = 1 x 2 − 1 x− −−−−√ f (x) = 1 x 2 − 1 x. clearly f(0) = 0 f (0) = 0. let's look at the derivative of f f. if we show that the derivative is strictly positive for x> 0 x> 0, the function is strictly increasing, hence positive (in combination with f(0) f (0)) for x> 0 x> 0. we. Theorem 8.6.1 leta be a realm×n matrix, and letσ1 ≥σ2 ≥···≥σr >0 be the positivesingular values ofa. thenr is the rank ofa and we have the factorization a=pΣaqt wherep andq are orthogonal matrices the factorization a =pΣaqt in theorem 8.6.1, where p and q are orthogonal matrices, is called a singular value decomposition (svd) of a. Free math problem solver answers your algebra homework questions with step by step explanations. Algebra. equation solver. step 1: enter the equation you want to solve into the editor. the equation calculator allows you to take a simple or complex equation and solve by best method possible. step 2: click the blue arrow to submit and see the result! the equation solver allows you to enter your problem and solve the equation to see the result.