Solved 8 453 653 Prove The Following Theorems If An Chegg

Solved 8 453 653 Prove The Following Theorems If An Chegg 8.7 prove the following theorems: (a) ( i∣0≤i≤n:i)=( i∣0≤i≤n∧ even.i: i) ( i∣0≤i≤ n∧ odd. i:i ) (b) ( i∣0≤i≤10:0)=0 your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Free math problem solver answers your algebra homework questions with step by step explanations.

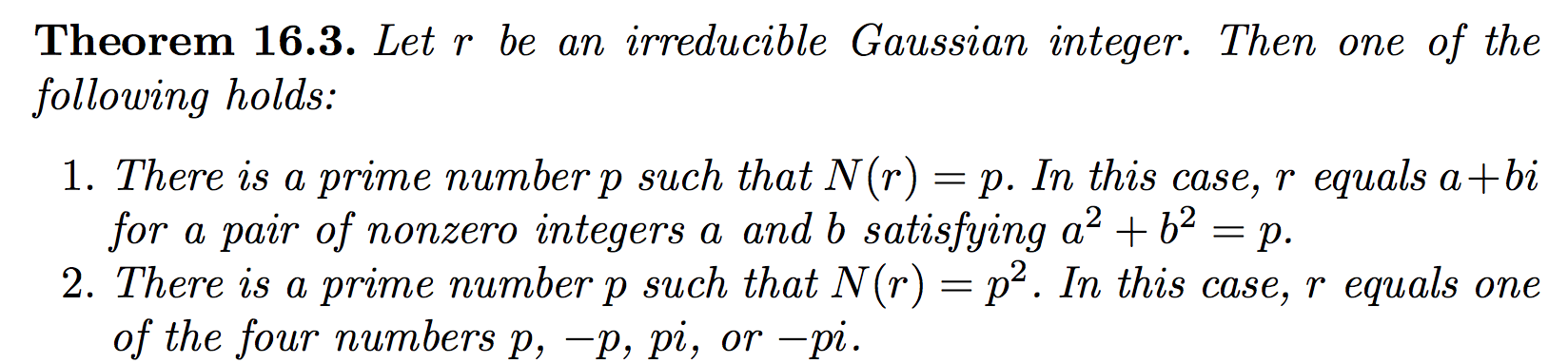
Solved Prove The Following Theorem Chegg Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. it shows you the solution, graph, detailed steps and explanations for each problem. symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and. Note that we added values (\(k\), \(l\), etc.) to each of the limits to make the proofs much easier.in these proofs we’ll be using the fact that we know \(\mathop {\lim }\limits {x \to a} f\left( x \right) = k\) and \(\mathop {\lim }\limits {x \to a} g\left( x \right) = l\) we’ll use the definition of the limit to make a statement about \(\left| {f\left( x \right) k} \right|\) and. Davneet singh has done his b.tech from indian institute of technology, kanpur. he has been teaching from the past 14 years. he provides courses for maths, science and computer science at teachoo. An indirect proof is used to prove theorems. prove the following theorem indirectly. we will give you a start. prove that a triangle cannot have two right angles. a triangle cannot have two right angles. suppose a triangle had two right angles. the sum of a triangle is 180 degrees. the two angles of a triangle would equal 180 degrees, which.

Solved Prove The Following Theorem Chegg Davneet singh has done his b.tech from indian institute of technology, kanpur. he has been teaching from the past 14 years. he provides courses for maths, science and computer science at teachoo. An indirect proof is used to prove theorems. prove the following theorem indirectly. we will give you a start. prove that a triangle cannot have two right angles. a triangle cannot have two right angles. suppose a triangle had two right angles. the sum of a triangle is 180 degrees. the two angles of a triangle would equal 180 degrees, which. Step 1: enter the equation you want to solve into the editor. the equation calculator allows you to take a simple or complex equation and solve by best method possible. step 2: click the blue arrow to submit and see the result! the solve for x calculator allows you to enter your problem and solve the equation to see the result. ( this is the method of adapting an existing proof.) 2)start with the premises, use axioms and known theorems to construct a proof that leads to the theorem. (this is forward reasoning) 3)to prove a theorem, find a different statement we can prove from which the theorem follows. (this is backwards reasoning.).

Solved Prove The Following Theorems You Should Start By Chegg Step 1: enter the equation you want to solve into the editor. the equation calculator allows you to take a simple or complex equation and solve by best method possible. step 2: click the blue arrow to submit and see the result! the solve for x calculator allows you to enter your problem and solve the equation to see the result. ( this is the method of adapting an existing proof.) 2)start with the premises, use axioms and known theorems to construct a proof that leads to the theorem. (this is forward reasoning) 3)to prove a theorem, find a different statement we can prove from which the theorem follows. (this is backwards reasoning.).