Solved 2 Find The Equations Of The Tangents To Circle X2 Y2 25 At

Solved 2 Find The Equations Of The Tangents To Circle X2 Y2 25 At Question: 2. consider the circle defined by x2 y2 = 25 (a) find the equations of the tangent lines to the circle at the points where x = 4. (b) find the equations of the normal lines to this circle at the same points. (the normal line is perpendicular to the tangent line at that point.) (c) at what point do the two normal lines intersect? 3. There are 3 steps to solve this one. example 1 (a) if x2 y2 25, find dy dx (b) find an equation of the tangent to the circle x2 y2 25 at the point (3, 4). solution 1 (a) differentiating both sides of the equation x2 y25 ) ) (25) dx dx d 2x 2y x dx 0. dx remembering that y is a function of x and using the chain rule, we have 2y dy dx.
The Equation Of The Tangents To The Circle X2 Y2 25 And Making Intercepts Question: find the equations of the lines tangent to the circle x2 y2=25 at the points where x= 4 in the xy plane. where do these (four) lines intersect and what is the shape and the area of the resulting quadrilateral? illustrate your results with a sketch of the circle and the tangents. Answer: the equation for the tangent line is y=2x 3. example 3: find the equation to the pair of tangents drawn from the origin to the circle x2 y2 4x 4y 7 = 0. solution: we use the relation obtained in the last example, t 2 = s s1, s 1, to write the desired equation. here, (x1,y1) (x 1, y 1) is (0, 0) while g = 2,f = 2 and c = 7. Free tangent line calculator find the equation of the tangent line given a point or the intercept step by step. I am given the equation of a circle: $(x 2)^2 (y 7)^2 = 25$. the radius is $5$. center of the circle: $( 2, 7)$. two lines tangent to this circle pass through point $(4, 3)$, which is outside of said circle. how would i go about finding one of the equations of the lines tangent to the circle?.

Solved You Are Given The Circle X2 Y2 25 A At What Chegg Free tangent line calculator find the equation of the tangent line given a point or the intercept step by step. I am given the equation of a circle: $(x 2)^2 (y 7)^2 = 25$. the radius is $5$. center of the circle: $( 2, 7)$. two lines tangent to this circle pass through point $(4, 3)$, which is outside of said circle. how would i go about finding one of the equations of the lines tangent to the circle?. 2) find the equations of the tangents to circle x2 y2 = 25 at the point (4 3) find the equations of the tangents to circle x2 y2 2x 6y 15 = 0 at the point (5 , 6) video answer get the answer to your homework problem. The circle c 1: x 2 y 2 = 3 having centre at origin,o intersects the parabola x 2 = 2 y at the point p in the first quadrant. let the tangent to the circle c 1 at p touches other two circles c 2 and c 3 at r 2 and r 3, respectively. suppose c 2 and c 3 have equal radii 2 √ 3 and centres q 2 and q 3, respectively. if q 2 and q 3 lie on the y.
Solved Example 4 Find The Equations Of The Tangents To The Circle X 2 2) find the equations of the tangents to circle x2 y2 = 25 at the point (4 3) find the equations of the tangents to circle x2 y2 2x 6y 15 = 0 at the point (5 , 6) video answer get the answer to your homework problem. The circle c 1: x 2 y 2 = 3 having centre at origin,o intersects the parabola x 2 = 2 y at the point p in the first quadrant. let the tangent to the circle c 1 at p touches other two circles c 2 and c 3 at r 2 and r 3, respectively. suppose c 2 and c 3 have equal radii 2 √ 3 and centres q 2 and q 3, respectively. if q 2 and q 3 lie on the y.
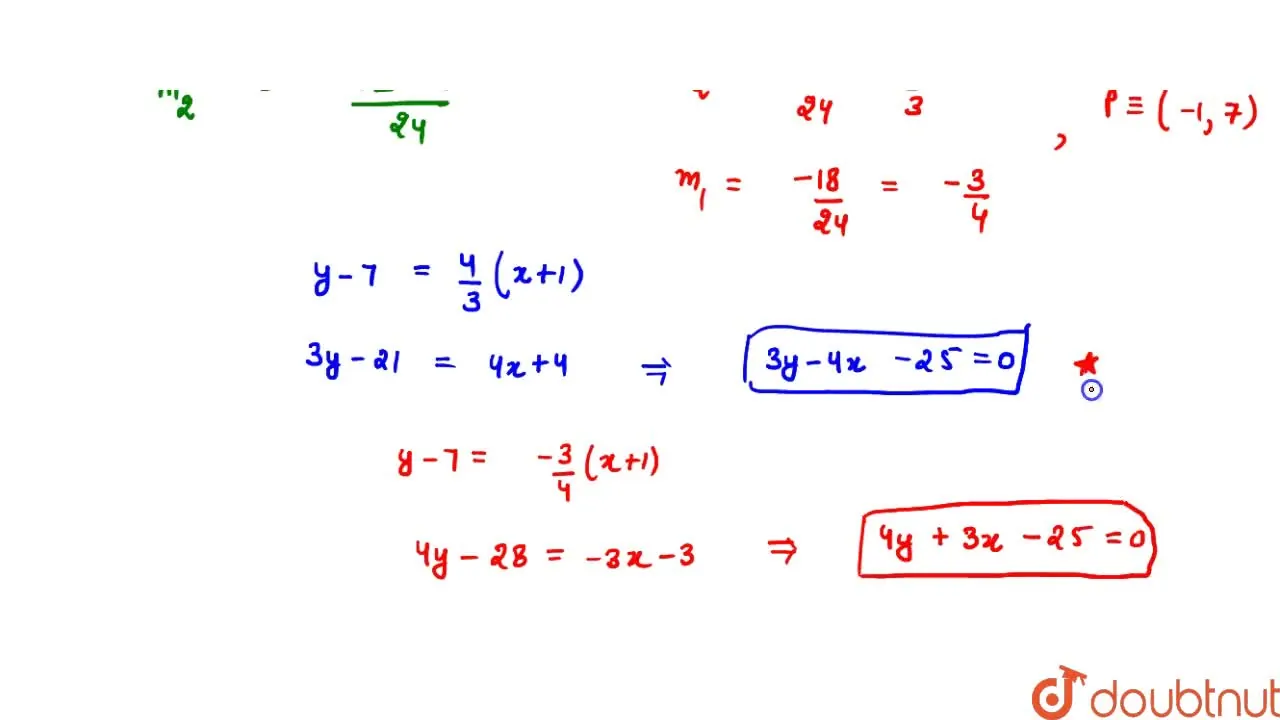
Find The Equations Of Tangents To The Circle X 2 Y 2 25 Which Pass
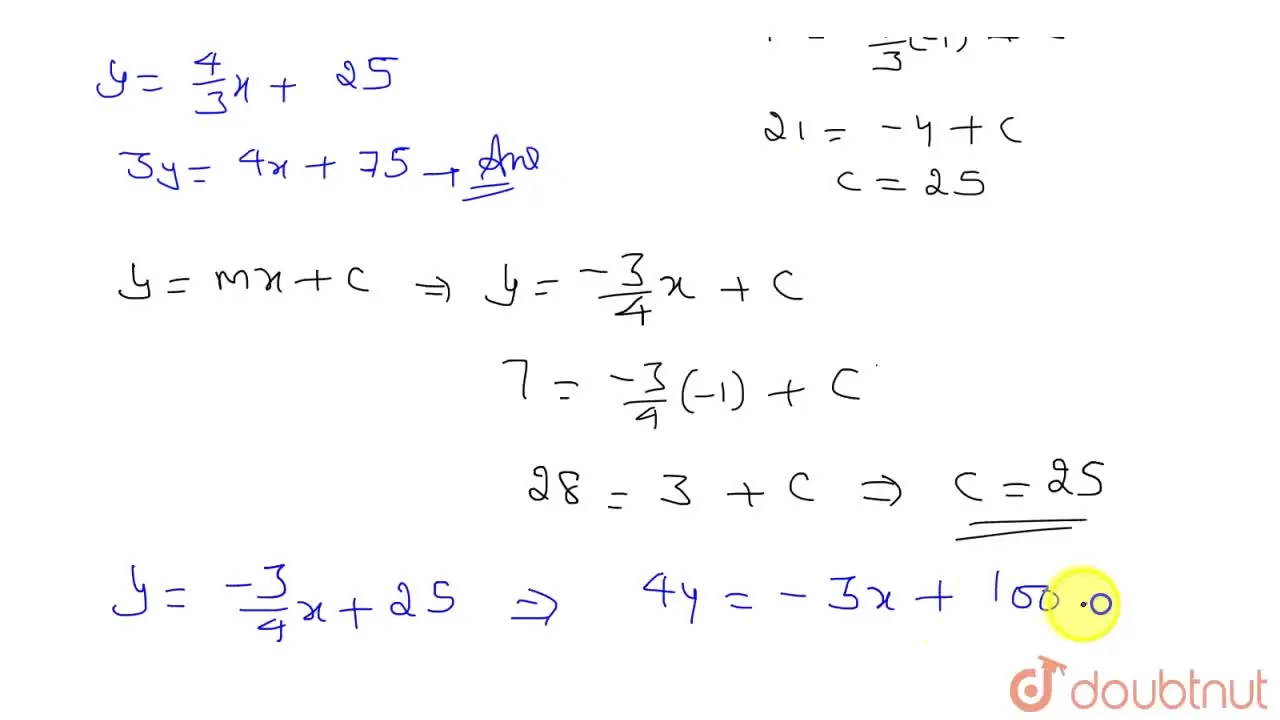
Find The Equations Of Tangents To The Circle X 2 Y 2 25 Which Pass

Comments are closed.