Solved 1 Prove The Following Identity By Using Mathematical Chegg Problem 1 [10] mathematical induction using mathematical induction, prove the following identity. ∑k=1n(k−1)k=(n3−n) 3. this problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. Question: 7. (a) prove the following identity by induction. ∑i=1ni (i 1)1=n 1n (b) in discussion 5 you proved an identity for the sum of consecutive square numbers. use the result from part a. to prove the following about the sum of reciprocal square numbers. you don't need induction for this part. ∑i=1ni21<2. there are 4 steps to solve.
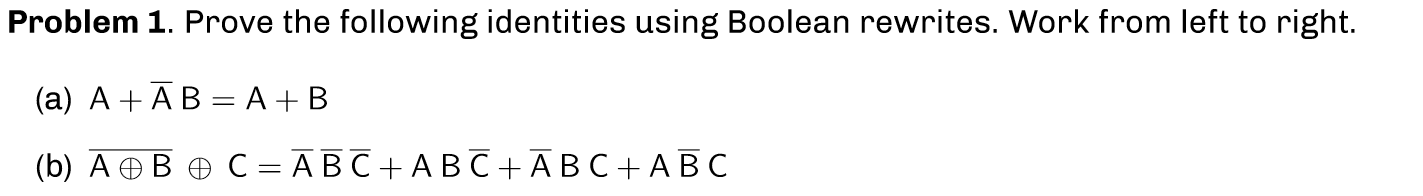
Solved Problem 1 Prove The Following Identities Using Chegg Use mathematical induction to prove the following identity for all n ∈ n. xn k=1 (k 1)2k = n2 n 1 your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. Thus far, we have learned how to use mathematical induction to prove identities. in general, we can use mathematical induction to prove a statement about \(n\). this statement can take the form of an identity, an inequality, or simply a verbal statement about \(n\). we shall learn more about mathematical induction in the next few sections. Proof by induction on n: step 1: prove that the equation is valid when n = 1. when n = 1, we have (2 (1) 1) = 12, so the statement holds for n = 1. step 2: assume that the equation is true for n, and prove that the equation is true for n 1. assume: 1 3 5 (2n 1) = n2. prove: 1 3 5 (2 (n 1) 1) = (n 1)2. For arbitrarily large n; since the determinant is a real nonnegative number, the only possibility is that. cos(θ)2 sin(θ)2 = 1. to get the details right, we select sequences of integers an, bn with. lim n → ∞anθ − 2πbn = 0 lim n → ∞an = ∞. e.g. this can be done by continued fractions.
Solved 1 Show The Following Identities Are True By Using Chegg Proof by induction on n: step 1: prove that the equation is valid when n = 1. when n = 1, we have (2 (1) 1) = 12, so the statement holds for n = 1. step 2: assume that the equation is true for n, and prove that the equation is true for n 1. assume: 1 3 5 (2n 1) = n2. prove: 1 3 5 (2 (n 1) 1) = (n 1)2. For arbitrarily large n; since the determinant is a real nonnegative number, the only possibility is that. cos(θ)2 sin(θ)2 = 1. to get the details right, we select sequences of integers an, bn with. lim n → ∞anθ − 2πbn = 0 lim n → ∞an = ∞. e.g. this can be done by continued fractions. Free trigonometric identity calculator verify trigonometric identities step by step prove\:\tan^2(x) \sin^2(x)=\tan^2(x)\sin^2(x) study tools ai math solver. Stack exchange network. stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Solved 1 Prove The Following Identities Using Simplified Chegg Free trigonometric identity calculator verify trigonometric identities step by step prove\:\tan^2(x) \sin^2(x)=\tan^2(x)\sin^2(x) study tools ai math solver. Stack exchange network. stack exchange network consists of 183 q&a communities including stack overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Solved Problem 1 Prove The Following Identities In All Chegg
Comments are closed.