Solution Differential Equations Method Of Solving First Order

First Order Differential Equations Teaching Resources The most general first order differential equation can be written as, dy dt = f (y,t) (1) (1) d y d t = f (y, t) as we will see in this chapter there is no general formula for the solution to (1) (1). what we will do instead is look at several special cases and see how to solve those. we will also look at some of the theory behind first order. A first order differential equation is an equation of the form f(t, y, ˙y) = 0. a solution of a first order differential equation is a function f(t) that makes f(t, f(t), f ′ (t)) = 0 for every value of t. here, f is a function of three variables which we label t, y, and ˙y. it is understood that ˙y will explicitly appear in the equation.

First Order Differential Equation Solutions Types Examples Step 4: solve the differential equation in u and x (that we got in the last step), using separation of variables method. find the value of u. step 5: place the value of u in the equation that we got in step 2. solve it to find v. step 6: now, as we know both u and v, just find the value of y (as y = uv). Since the initial current is 0, this result gives an initial condition of i(0) = 0. we can solve this initial value problem using the five step strategy for solving first order differential equations. step 1. rewrite the differential equation as i′ 12.5i = 125sin20t. this gives p(t) = 12.5 and q(t) = 125sin20t. Linear. a first order differential equation is linear when it can be made to look like this: dy dx p (x)y = q (x) where p (x) and q (x) are functions of x. to solve it there is a special method: we invent two new functions of x, call them u and v, and say that y=uv. we then solve to find u, and then find v, and tidy up and we are done!. Often, a first order ode that is neither separable nor linear can be simplified to one of these types by making a change of variables. here are some important examples: homogeneous equation of order 0: dy dx = f(x, y) where f(kx, ky) = f(x, y). use the change of variables z = y x to convert the ode to xdz dx = f(1, z) − z, which is separable.
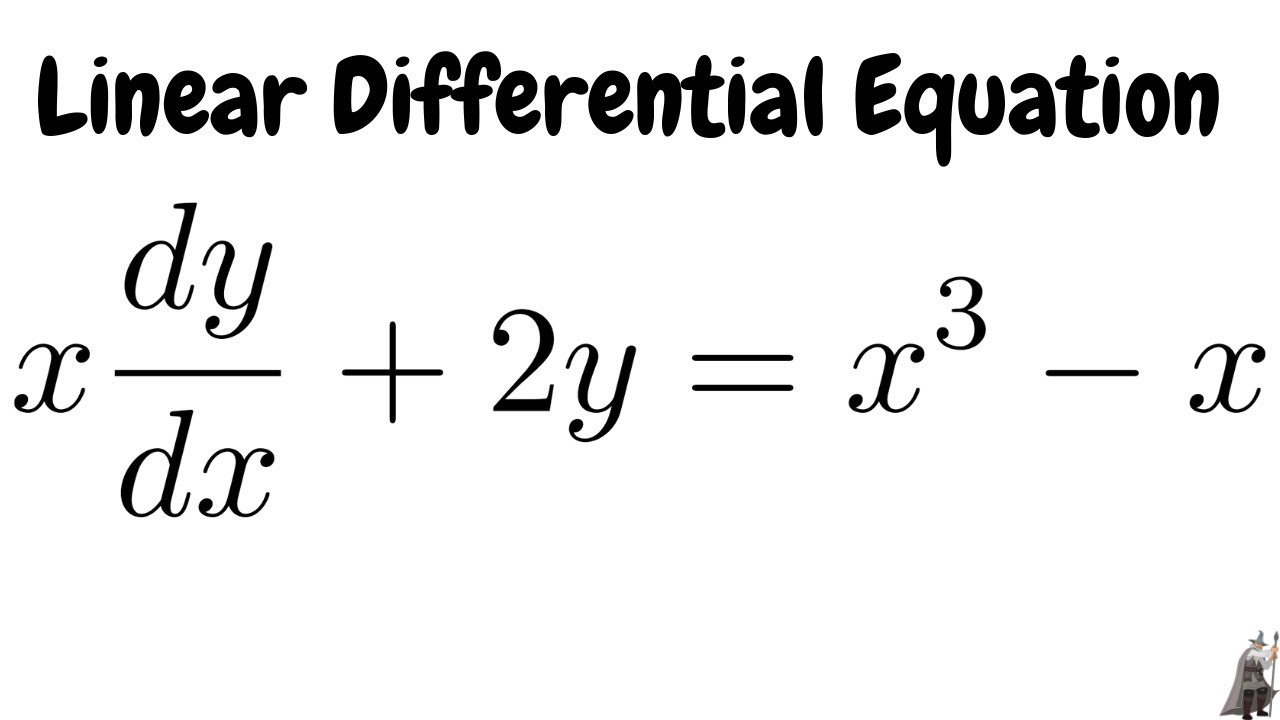
Solving A First Order Linear Differential Equation Youtube Linear. a first order differential equation is linear when it can be made to look like this: dy dx p (x)y = q (x) where p (x) and q (x) are functions of x. to solve it there is a special method: we invent two new functions of x, call them u and v, and say that y=uv. we then solve to find u, and then find v, and tidy up and we are done!. Often, a first order ode that is neither separable nor linear can be simplified to one of these types by making a change of variables. here are some important examples: homogeneous equation of order 0: dy dx = f(x, y) where f(kx, ky) = f(x, y). use the change of variables z = y x to convert the ode to xdz dx = f(1, z) − z, which is separable. Ferential equation to a system of ordinary differential equations. we can use ode theory to solve the characteristic equations, then piece together these characteristic curves to form a surface. such a surface will provide us with a solution to our pde. example 1. find a solution to the transport equation, ut aux = 0: (2.3). In this section we solve linear first order differential equations, i.e. differential equations in the form y' p(t) y = g(t). we give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process.

First Order Linear Differential Equations Youtube Ferential equation to a system of ordinary differential equations. we can use ode theory to solve the characteristic equations, then piece together these characteristic curves to form a surface. such a surface will provide us with a solution to our pde. example 1. find a solution to the transport equation, ut aux = 0: (2.3). In this section we solve linear first order differential equations, i.e. differential equations in the form y' p(t) y = g(t). we give an in depth overview of the process used to solve this type of differential equation as well as a derivation of the formula needed for the integrating factor used in the solution process.

Comments are closed.